Simplex

In matematica , e più in particolare in geometria , un simplesso è una generalizzazione del triangolo a qualsiasi dimensione .

Definizione

In geometria , un simplesso o n -simplex è l'analogo n- dimensionale del triangolo. Deve il suo nome al fatto che è l'oggetto geometrico chiuso “più semplice” che ha n dimensioni. Ad esempio su una linea (1 dimensione) l'oggetto monodimensionale più semplice è il segmento , mentre nel piano (2 dimensioni) l'oggetto geometrico chiuso bidimensionale più semplice è il triangolo, e nello spazio (3 dimensioni) il chiuso più semplice oggetto geometrico in 3 dimensioni è il tetraedro (piramide a base triangolare).

Più esattamente, un simplesso è l' inviluppo convesso di un insieme di ( n +1) punti utilizzati per formare un sistema di coordinate affine in uno spazio affine di dimensione n , il che significa che:

su una retta si farà riferimento ad un'origine e ad 1 punto (generalmente un riferimento (O, I) , che definisce l'unità dell'asse), e [OI] è un segmento .
nel piano il riferimento sarà costituito da un'origine e 2 punti (generalmente un riferimento (O, I, J) , che definisce l'unità per ogni asse), e OIJ è un triangolo .
nello spazio il sistema di coordinate sarà costituito da un'origine e 3 punti (generalmente un sistema di coordinate (O, I, J, K) , che definisce l'unità per ciascun asse), e OIJK è un tetraedro .

Le coordinate dei vertici del simplesso (nel sistema di coordinate formato dai suoi vertici) sono quindi:

e 0 = (0, 0, 0,…, 0), e 1 = (1, 0, 0,…, 0), e 2 = (0, 1, 0,…, 0),

\ vdots

e n = (0, 0, 0,…, 1)

Tuttavia, per motivi di simmetria tra i vertici, si preferisce spesso immergere il simplesso in un iperpiano affine dello spazio di dimensione n +1, attribuendo a ciascun vertice le seguenti coordinate n +1:

e 0 = (1, 0, 0, 0,…, 0), e 1 = (0, 1, 0, 0,…, 0), e 2 = (0, 0, 1, 0,…, 0),

\ vdots

e n = (0, 0, 0, 0,…, 1)

Il numero n è chiamato la dimensione o il grado o anche l' ordine del n- simplex s . Ad esempio, uno 0-simplex è un punto , un 1-simplex è un segmento, un 2-simplex è un triangolo, un 3-simplex è un tetraedro, un 4-simplex è un pentacoro (o pentatopo), ecc. Poiché il simplesso 0-dimensionale è un singleton , all'insieme vuoto viene talvolta assegnata la dimensione –1.

Sia s quindi un simplesso formato dai punti a 0 ..., a n . Un punto x di s si scrive in modo univoco:

x = \ somma _ {{i = 0}} ^ {n} {t_ {i} a_ {i}}

dove t i sono i positivi o nulli coordinate baricentriche di x rispetto ad un 0 ..., un n . Si noti la somiglianza tra questa formula e quella dell'equilibrio di un oggetto nella meccanica statica fisica : la quale afferma che la somma delle forze esterne applicate a un oggetto in equilibrio è uguale al vettore zero. Ciò deriva dal fatto che l'oggetto, qualunque sia l'intensità di queste n forze che lo tirano (che possono essere rappresentate come n molle attaccate all'oggetto e agli n vertici di a ( n - 1) - simplex), rimarrà sempre in questo simplesso: qualsiasi punto del simplesso può essere definito da queste forze che lo attraggono più o meno verso questo o quel vertice, da qui l'uso della nozione di baricentro . Si noterà anche che, affinché un oggetto sia in equilibrio, deve necessariamente trovarsi nel simplesso formato dai punti che lo attraggono. ${\ displaystyle \ sum {{\ vec {F}} _ {ext}} = {\ vec {0}}}$

Un simplesso regolare è un simplesso che è anche un politopo regolare (cioè tutti i suoi bordi sono della stessa lunghezza, le sue facce sono della stessa natura geometrica e sono organizzate allo stesso modo nelle stesse quantità in ogni vertice).

La parola “simplex” fu data da Pieter Hendrik Schoute nel 1902 , ma Ludwig Schläfli aveva già dimostrato l'esistenza di simplessi regolari per qualsiasi dimensione n (quindi semplicemente simplessi) quando dimostrò che c'erano sempre a meno tre politopi regolari per qualsiasi dimensione maggiore di 3 (vale a dire n -simplex, così come n - ipercubo e n - iperottaedro ).

Elementi

Gli elementi di un simplesso sono chiamati n -facce , dove n è la loro dimensione:

Le 0-facce sono chiamate vertici
1-facce sono chiamate bordi
2-facce sono chiamate facce
le 3 facce sono chiamate cellule

Le ( n -1) -facce di un n -simplex formano il suo inviluppo .

Le n -facce di un simplesso sono esse stesse simplessi di dimensioni più piccole. Ad esempio, un tetraedro ha facce triangolari.

Quando elenchiamo le n -facce dei simplessi e il loro numero, otteniamo un triangolo di Pascal :

Simplex	Numero di vertici	Numero di bordi	Numero di facce	Numero di celle	Numero di 4 lati	Numero di 5 lati	Numero di 6 lati
Punto	1	-	-	-	-	-	-
Segmento	2	1	-	-	-	-	-
Triangolo	3	3	1	-	-	-	-
tetraedro	4	6	4	1	-	-	-
pentacore	5	10	10	5	1	-	-
5 simplex	6	15	20	15	6	1	-
6 simplex	7	21	35	35	21	7	1
...

Il triangolo di Pascal, una delle cui caratteristiche è che la seconda colonna corrisponde a ciascun numero triangolare , la terza a ciascun numero tetraedrico , la quarta a ciascun numero pentatopico ...

Il numero di vertici di un n -simplex è uguale e il numero di n -facce è sempre valido perché è il simplesso stesso. Il numero di archi di un n -simplex vale , perché è circa il numero di coppie di vertici diversi che si possono raggiungere. ${\ stile di visualizzazione N_ {0} = n + 1}$ ${\ displaystyle N_ {n} = 1}$ ${\ displaystyle N_ {1} = {\ frac {n (n + 1)} {2}}}$

Tra i numeri di ciascun elemento di un simplesso esiste una relazione di Eulero in cui, sommando gli elementi di dimensione pari (vertici, facce, 4-facce, 6-facce...) e sottraendo gli elementi di dimensione dispari (spigoli, celle, 5-facce, 7-facce…), si ottiene la caratteristica di Eulero-Poincaré del simplesso, che vale 0 per i simplessi di grado pari e 2 per i simplessi di grado dispari:

${\ displaystyle \ sum _ {i = 0} ^ {n-1} N_ {i} \ volte (-1) ^ {i} = N_ {0} -N_ {1} + N_ {2} -N_ {3 } + ... + N_ {n-1} (- 1) ^ {n-1} = 1 - (- 1) ^ {n}}$ , dove è il numero di ( n - 1) -facce (usiamo n - 1 nella formula invece di n per non contare l' n -simplex stesso e fermarci ai suoi elementi rigorosi). $N _ {{n-1}}$

Per il segmento: 2 punti = 2
Per il triangolo: 3 punti - 3 spigoli = 0
Per il tetraedro: 4 punti - 6 spigoli + 4 facce = 2
Per il pentacore: 5 punti - 10 spigoli + 10 facce - 5 celle = 0

rappresentazioni

Poiché gli n -simplex spesso hanno più dimensioni degli oggetti che siamo abituati a vedere nella vita di tutti i giorni, usiamo diversi mezzi di rappresentazione per lavorare con loro più facilmente. Tra queste rappresentazioni, usiamo spesso le proiezioni di un n -simplex in uno spazio dimensionale inferiore (di solito 2 o 3).

È impossibile rappresentare perfettamente un oggetto in uno spazio che ha meno dimensioni di esso, quindi dobbiamo usare queste rappresentazioni con cautela, alcune distorcono le lunghezze, gli angoli, persino la struttura del simplesso, oppure ci fanno vedere segmenti che si intersecano quando in realtà non si intersecano.

Grafici

La rappresentazione bidimensionale di un n- simplex è un grafo completo . Per disegnare il grafico di un n -simplex basta collegarli tutti n + 1 punti.

Quando si ha a che fare con il grafico di un simplesso di cui non si conosce il grado, è sufficiente contare il numero di segmenti che sono collegati a un vertice.

Per passare dal grafico di un n -simplex a quello di un ( n + 1) -simplex, aggiungiamo un nuovo punto e colleghiamo ad esso tutti gli altri.

Grafici dei primi simplessi

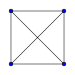
Simplex	Segmento	Triangolo	tetraedro	Pentatope	5 simplex	6 simplex	7 simplex
Dimensione	1	2	3	4	5	6	7
vertici	2	3	4	5	6	7	8
Grafico

Attenzione: il grafico essendo solo una proiezione del n -simplex su un piano, come un ombra , le lunghezze e gli angoli non sono rispettati: è necessario immaginare che tutti i segmenti sono della stessa lunghezza, e che tutti i triangoli che collegano 3 vertici sono equilateri se il simplesso è regolare. Inoltre, le diagonali del grafico non si incontrano mai effettivamente, ma passano davanti o dietro le altre.

Un grafo come questi è chiamato anche poligono di Petrie perché è ottenuto dalla proiezione ortogonale di un politopo su un piano.

Diagramma di Coxeter-Dynkin

Il diagramma di Coxeter-Dynkin di un n -simplex è nella forma: … , con n cerchi (chiamati nodi ) nella catena.

Schläfli simbolo

Il simbolo Schläfli di un n -simplex è {3,3,3, ..., 3,3}, con n - 1 per il numero 3.

Proprietà

Qualsiasi k -simplex generato da un sottoinsieme di { a 0 , a 1 ,…, a n } (che sono i vertici del simplesso s ) è detto k -face di s .
L'insieme delle facce di s diverse da s stesso sono dette facce proprie di s , e la loro unione è detta arco di s .
Un n -simplex non ha diagonali perché per definizione, gli n + 1 vertici di un n -simplex sono già collegati tra loro.
L' isobaricentro di un n -simplex si trova al centro delle sue ( n - 1) -facce. Ad esempio l'isobaricentro di un segmento si trova a 1/2 dei suoi estremi, l'isobaricentro di un triangolo equilatero si trova a 1/3 dei punti medi dei suoi lati, l'isobaricentro di un tetraedro si trova a 1/4 dei centri dei volti... ${\ displaystyle {\ frac {1} {n + 1}}}$
Un simplesso è il suo stesso duale , il che significa che quando colleghiamo insieme tutti i centri delle ( n - 1) -facce di un n -simplex, ricadiamo sullo stesso simplesso, ridotto della metà.
Se un simplesso ha un “angolo destro” (vale a dire che tutti gli spigoli che si incontrano in un vertice sono perpendicolari in essi), possiamo allora usare la generalizzazione n- dimensionale del teorema di Pitagora : “La somma dei quadrati di ( n –1) -volumi di iperfacce adiacenti all'angolo destro è uguale al quadrato di ( n –1) -volume opposto all'angolo destro ”. Ad esempio, in un triangolo rettangolo ABC in A abbiamo , in una piramide ABCD rettangolo in A abbiamo , e in un pentatopo ABCDE rettangolo in A abbiamo . $AC ^ {2} = AB ^ {2} + AC ^ {2}$ $BCD ^ {2} = ABC ^ {2} + ABD ^ {2} + ACD ^ {2}$ $BCDE ^ {2} = ABCD ^ {2} + ABCE ^ {2} + ABDE ^ {2} + ACDE ^ {2}$
Topologicamente , un n -simplex è omeomorfo a un n -sphere. Ogni n -simplex è una varietà convessa senza fori di dimensione n . La caratteristica di Eulero di qualsiasi n -simplex vale quindi 0 se n è pari e 2 se n è dispari, come per la n -sfera.
Il gruppo di isometrie del regolare n -simplex è il gruppo simmetrico S n + 1 .

Lunghezze e volume notevoli del normale n -simplex

L'altezza del n -simplex regolare dello spigolo $a$ è: ${\ displaystyle h_ {n} = a {\ sqrt {\ frac {n + 1} {2n}}}}$ ;
il raggio dell'ipersfera circoscritta è: ${\ displaystyle R_ {n} = a {\ sqrt {\ frac {2n} {n + 1}}}}$ ;
il raggio dell'ipersfera inscritta è: $r_n = \ frac a {\ sqrt {2n (n + 1)}}$ .

Dimostrazione

${\ displaystyle h_ {n} = R_ {n} + r_ {n}}$ .
$h_ {n} ^ {2} + R _ {{n-1}} ^ {2} = a ^ {2}$ perché l'altezza è perpendicolare a qualsiasi retta della ( n - 1) -base, quindi anche al raggio della ( n - 1) -sfera circoscritta dalla ( n - 1) -base, e il bordo di lunghezza a collega il vertice dell'altezza con un vertice della base, i tre formano un triangolo rettangolo, applichiamo semplicemente il teorema di Pitagora .
$R_ {n} ^ {2} = r_ {n} ^ {2} + R _ {{n-1}} ^ {2}$ poiché il raggio dell'n -sfera circoscritta collega il centro dell'n -simplex ad un vertice, il raggio della sfera inscritta collega il centro dell'n -simplex al centro della base (poiché l' n -sfera inscritta è tangente al n - simplex questo raggio è perpendicolare alla base), e il raggio del ( n - 1) -sphere circoscritta alla base collega il centro della base ad un vertice del n -simplex, ancora applichiamo Pitagora teorema.

Per induzione, da , si ottengono le formule annunciate. ${\ stile di visualizzazione R_ {1} = a}$

Ogni simplesso ha un ipervolume che corrisponde al suo interno (per il segmento è la sua lunghezza , per il triangolo della sua area , per il tetraedro del suo volume ). L' n -volume di un n -simplex è il prodotto di un'altezza (distanza tra un vertice e il centro della ( n - 1) -faccia opposta) e la base corrispondente (( n - 1) -volume di questa ( n - 1) -faccia), diviso per la dimensione del simplesso.
Se indichiamo con $V n$ l' n -volume del regolare n -simplex dell'arco $a$ , abbiamo quindi:

{\ displaystyle V_ {n} = {\ frac {h_ {n} V_ {n-1}} {n}}}

Per induzione, dalla lunghezza di un segmento ( ) e dall'espressione precedente per , deduciamo: $V_ {1} = a$ $h_ {n}$

V_ {n} = {\ frac {a ^ {n}} {n!}} \ Times {\ sqrt {\ frac {n + 1} {2 ^ {n}}}}

. Esempi:

l'area del triangolo equilatero è: ; ${\ displaystyle V_ {2} = {\ frac {a ^ {2} {\ sqrt {3}}} {4}} \ circa a ^ {2} \ volte 0 {,} 433}$
il volume del tetraedro regolare è: ; ${\ displaystyle V_ {3} = {\ frac {a ^ {3} {\ sqrt {2}}} {12}} \ circa a ^ {3} \ volte 0 {,} 118}$
ipervolume il pentacore regolare è: . ${\ displaystyle V_ {4} = {\ frac {a ^ {4} {\ sqrt {5}}} {96}} \ circa a ^ {4} \ volte 0 {,} 023}$