Omotopia

In matematica , un'omotopia è una deformazione continua tra due mappature, in particolare tra percorsi con estremità fisse e in particolare lacci . Questa nozione topologica consente di definire invarianti algebriche utilizzate per classificare mappature continue tra spazi topologici , nell'ambito della topologia algebrica .

L'omotopia induce una relazione di equivalenza su mappe continue, compatibile con la composizione , che porta alla definizione dell'equivalenza di omotopia tra spazi topologici.

L'omotopia fornisce informazioni sulla natura topologica di uno spazio. Una fascia circolare di un piano non può essere equivalente , nel senso di omeomorfismo , a un disco . In un disco, ogni pizzo è omotopico in un punto. In una fascia circolare, questo non è il caso. Questa osservazione è una fonte di prove, come quelle del teorema di d'Alembert-Gauss , del punto fisso di Brouwer , di Borsuk-Ulam o anche quella del teorema del sandwich di prosciutto che specifica ad esempio che tre solidi misurabili e misure finite di dato lo spazio normale , c'è un piano che separa ciascuno dei solidi in due parti di uguali misure.

Definizione

È una classe di equivalenza del percorso per la relazione di omotopia.

Sia X uno spazio topologico. Un percorso γ continua di X è una mappatura continua del reale segmento [0, 1] in X . Questa definizione corrisponde all'idea intuitiva di percorso , nel senso di un percorso che parte da un punto γ (0) per arrivare ad un altro punto γ (1).
Due cammini continui γ 0 e γ 1 di X sono espressi omotopici quando c'è un'applicazione continua H di [0, 1] 2 in X tale che l'applicazione a t combina H ( t , 0) è uguale a γ 0 e che a t combina H ( t , 1) è uguale a γ 1 . Formalmente: $\ forall t \ in [0,1] \ quad H (t, 0) = \ gamma _ {0} (t) {\ text {et}} H (t, 1) = \ gamma _ {1} (t )$
Questa situazione non descrive ancora con precisione la situazione mostrata a destra. Nell'illustrazione, i due percorsi γ 0 e γ 1 hanno la stessa origine x e la stessa estremità y . Cioè :
$\ gamma _ {0} (0) = \ gamma _ {1} (0) = x {\ text {e}} \ gamma _ {0} (1) = \ gamma _ {1} (1) = y.$ Due cammini continui γ 0 e γ 1 di X aventi la stessa origine e la stessa estremità sono detti strettamente omotopici quando sono omotopici dell'omotopia H e che, per ogni elemento s di [0, 1]: $H (0, s) = x {\ text {e}} H (1, s) = y.$

Le definizioni di cui sopra generalizzano a due funzioni continue f e g di uno spazio topologico X in uno spazio topologico Y .
Le due funzioni f e g sono detti omotopi , homotopy H , se H è una funzione continua di X × [0, 1] in Y tale che la mappa che ad x associa H (x, 0) è uguale a f e in cui x associa H (x, 1) è uguale a g .
È possibile generalizzare la seconda definizione. Lasciate Un essere un sottoinsieme di X tale che le restrizioni di f e g di A sono uguali.
Le due funzioni f e g si dice che siano omotopi rispetto ad A se f e g sono omotopi, omotopi H e che: $\ forall s \ in [0,1], \; \ forall a \ in A \ quad H (a, s) = f (a) = g (a)$

Esempi

Spazio contrattile

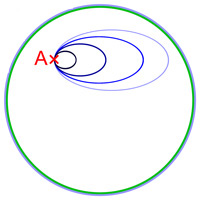
Uno spazio X si dice contrattile se la sua mappa di identità id X è omotopica a una mappa costante, o ancora: se una mappa continua di uno spazio Y in X è omotopica a una mappa costante.

In particolare, uno spazio contrattile è semplicemente connesso :

Qualsiasi imbardata di uno spazio contrattile è omotopica a un'imbardata costante.

In uno spazio vettoriale normalizzato (o più in generale: uno spazio vettoriale topologico ) su ℝ, qualsiasi parte stellata , in particolare qualsiasi convesso non vuoto, è contrattile. La figura a destra illustra il caso di un pizzo in un disco . Questo pizzo è visibilmente omotopico "in un punto", vale a dire in un laccio costante.

Cerchio

Nel caso di un cerchio S 1 , qui identificato con i complessi di modulo 1, la situazione non è equivalente alla precedente. Intuitivamente, se un filo scorre ad anello attorno a un cerchio, non è possibile modificare il "numero di giri" (contato algebricamente) senza che il filo esca dalla superficie del cerchio e senza romperlo. Questo numero di turni è formalmente definito come segue. La mappa ℝ → S 1 , t ↦ exp ( $i2π$ t ) essendo un $omeomorfismo$ locale , qualsiasi imbardata $γ$ : [0, 1] → S 1 tale che $γ$ (0) = $γ$ (1) = 1 ha un unico orientamento continuo tale quello , e il grado di imbardata $γ$ è quindi il numero intero . Se due di tali cicli sono omotopici, dimostriamo (annotando in modo simile questa omotopia) che hanno lo stesso grado. Infatti, lungo l'omotopia, il grado varia continuamente e assume solo valori interi, quindi è costante. $\ scriptstyle {\ tilde \ gamma}: [0,1] \ a \ mathbb {R}$ $\ scriptstyle {\ tilde \ gamma} (0) = 0$ $\ scriptstyle {\ tilde \ gamma} (1)$

Ad esempio, il laccio che in t combina exp ( $i2π$ t ), grado 1, non è omotopico al ciclo costante a quel t associa 1 0 gradi.

Utilizza

Teorema di D'Alembert-Gauss

L'omotopia è la fonte di molte dimostrazioni. Un famoso esempio è il teorema di d'Alembert-Gauss , che indica che ogni polinomio non costante con coefficienti complessi ha almeno una radice in ℂ.

Per dimostrarlo, consideriamo un polinomio unitario P senza radice in ℂ e dimostreremo che il suo grado n è zero. Per ogni r reale positivo , definiamo l'imbardata α r da:

\ forall t \ in [0,1] \ quad \ alpha _ {r} (t) = {\ frac {P (r \ exp (2 \ pi {\ mathrm i} t)) / P (r)} { | P (r \ exp (2 \ pi {\ mathrm i} t)) / P (r) |}}.

Per definizione, α r è un laccio definito sul cerchio. Se r è uguale a 0, otteniamo il ciclo costante uguale a 1. Poiché la funzione che associa α r ( t ) a r e t è continua, tutti i cicli α r sono omotopici in un punto.

Sia ( a j ) la successione dei coefficienti di P e ρ un numero reale maggiore di 1 e che la somma Σ | a j | di moduli coefficienti di P . Se z è un complesso di modulo ρ,

(1) \ quad | z ^ {n} | = \ rho ^ {n}> (| a_ {0} | + \ cdots + | a _ {{n-1}} |) \ rho ^ {{n- 1}} \ geq | a_ {0} + a_ {1} z + \ cdots + a _ {{n-1}} z ^ {{n-1}} |.

Definiamo il polinomio P s e il ciclo β s da:

P_ {s} (z) = s (a_ {0} + a_ {1} z + \ cdots + a _ {{n-1}} z ^ {{n-1}}) + z ^ {n}, \ quad \ forall t \ in [0,1] \ quad \ beta _ {s} (t) = {\ frac {P_ {s} (\ rho \ exp (2 \ pi {\ mathrm i} t)) / P_ {s} (\ rho)} {| P_ {s} (\ rho \ exp (2 \ pi {\ mathrm i} t)) / P_ {s} (\ rho) |}}.

Le disuguaglianze (1) mostrano che se | s | ≤ 1, il polinomio P s non ammette una radice di modulo ρ quindi l'anello β s è ben definito . L'imbardata β 0 fa n giri attorno all'origine, secondo il paragrafo precedente. Poiché la funzione che associa β s ( t ) con s e t è continua, questo ciclo β 0 è omotopi per β 1 = alfa P . Poiché quest'ultimo è omotopico in un punto, cioè fa 0 giri attorno all'origine, n è effettivamente uguale a 0.

Gruppo fondamentale

Se X è uno spazio topologico, possiamo comporre due anelli della stessa base p (cioè della stessa origine e della stessa estremità p ) α 1 e α 2 costruendo un anello che attraversa prima la traiettoria di α 1 , quindi quello di α 2 . Questa composizione è compatibile con la relazione di equivalenza a cui è omotopica . Quozienti da questa relazione di equivalenza, otteniamo una struttura di gruppo chiamata gruppo fondamentale o gruppo di Poincaré . Questa nozione è generalizzata e consente di definire un'infinità di gruppi di omotopia .

Questo gruppo è all'origine delle manifestazioni. Uno dei più famosi è quello del teorema del punto fisso di Brouwer in dimensione due, che indica che qualsiasi mappa continua del disco ammette di per sé un punto fisso.

Topologia algebrica

L'omotopia è uno degli strumenti essenziali della topologia algebrica. Il caso più semplice, quello dei lacci, è fonte di molte dimostrazioni in questo campo. Oltre al teorema di d'Alembert-Gauss oa quello del punto fisso di Brouwer, quello di Borsuk-Ulam è caratteristico di un approccio di topologia algebrica. Nella dimensione due, indica che qualsiasi mappa continua della sfera in ℝ 2 ammette due punti antipodali della stessa immagine. In altre parole, ci sono sempre due punti sulla terra situati agli antipodi che hanno esattamente la stessa temperatura e la stessa pressione. Risolve in senso affermativo alcune famose domande come quella del panino al prosciutto : esiste un piano che taglia tre solidi delimitati e misurabili (corrispondenti al prosciutto, al formaggio e al pane di un panino ) in due parti di volumi uguali per i tre solidi? I ragionamenti di topologia algebrica che utilizzano l'omotopia permettono anche di dimostrare che se tre unità chiuse hanno la sfera come unione, almeno una di esse contiene due punti antipodali.

Possiamo anche citare la questione della condivisione della collana e dei due ladroni: una collana aperta, mostrata a sinistra, è composta da perle di due diversi colori, con un numero pari di perle di ogni colore. Viene mostrato in modo basilare che i due ladri possono distribuire uniformemente le perle tagliando la collana con solo due forbici. Il teorema di Borsuk-Ulam ci permette di dimostrare che più in generale, se ci sono t colori di perle, sono sufficienti t tagli.

La nozione di omotopia tra due funzioni consente di definire una relazione di equivalenza tra spazi topologici:

Due spazi E e F sono detti homotopically equivalente (o “dello stesso tipo di omotopia”) se ci sono due continui mappe f : E → F e g : F → E tale che g ∘ f IS omotopi per id E e f ∘ g IS omotopi a id F .

Uno spazio è contrattile se e solo se ha lo stesso tipo di omotopia di un singoletto .

Due spazi topologici omeomorfi sono omotopicamente equivalenti ma il contrario è falso, come mostrato dai seguenti esempi:

a parte il punto stesso, gli spazi contrattili non sono omeomorfi (e neppure equipotenti ) nel punto;
un cerchio è omotopicamente equivalente a ℂ * cioè un piano privo di un punto, ma non gli è omeomorfo (il cerchio privo di due punti non è connesso , mentre il piano privo di tre punti ad est);
un intervallo reale , un disco nel piano o una palla in ℝ 3 , aperti o chiusi, sono, tutti e sei, contrattili e quindi omotopicamente equivalenti, ma a due a due non omeomorfi (per analoghi argomenti di connessione o di semplice connessione , anche - distinguere aperto da chiuso - compatto ).

Varie proprietà importanti nella topologia algebrica sono preservate dall'equivalenza dell'omotopia, tra cui: la connettività semplice, la connettività per archi , i gruppi di omotopia , i gruppi di omologia e la coomologia ...

L' isotopia è un perfezionamento dell'omotopia; nel caso in cui le due $mappe$ continue $f$ $,$ $g$ $:$ $X$ $\to$ $Y$ siano omeomorfismi , potremmo voler andare da $f$ a $g$ non solo in modo continuo ma anche per omeomorfismi.

Faremo quindi diciamo che $f$ e $g$ sono isotopi se esiste una funzione continua $H : X \times [0, 1] \to Y$ tale che:

$\ forall x \ in X, \, H (x, 0) = f (x) \, \!$ ;

$\ forall x \ in X, \, H (x, 1) = g (x) \, \!$ ;

per tutto l'applicazione è un omeomorfismo. $t \ in [0,1]$ $X \ su Y, ~ x \ mappa su H (x, t)$

Una variante è la nozione di isotopia ambientale , che è una sorta di deformazione continua dello "spazio ambientale", trasformando progressivamente un sottospazio in un altro: due incorporamenti $α, β$ di uno spazio Z in uno spazio X sono noti come "isotopi ambientali" se si estendono in due omeomorfismi $f , g$ di X in sé isotopi (nel senso precedente) o, che è equivalente, se esiste un'isotopia tra l' identità di X e un omeomorfismo h di X di per sé tale che h ∘ $α = β$ . Questa nozione è importante nella teoria dei nodi: si dice che due nodi sono equivalenti se sono collegati da un'isotopia ambientale.

Ad esempio, l'effetto di parallasse produce un'isotopia ambientale delle viste prospettiche degli oggetti.

Note e riferimenti

Questa definizione può essere trovato in particolare: L. Borel e P. Weiss, Un primo approccio homotopy nell'ambito continuo , ENST Master .
troviamo questa definizione a Jean Lannes , “ Fundamental Group ” ( Archivio • Wikiwix • Archive.is • Google • Cosa fare? ) , École Polytechnique,2004, p. 13.
Troviamo un approccio più completo che rende possibile determinare il gruppo fondamentale del cerchio in Lannes 2004 , p. 8 o (en) Allen Hatcher , Topologia algebrica , New York, CUP ,2001, 544 p. ( ISBN 978-0-521-79540-1 , leggi online ) , p. 29.
Hatcher 2001 , p. 31
Lannes 2004 , p. 5
Lannes 2004 , p. 11
omotopia è descritta come l' idea principale della topologia algebrica in Hatcher 2001 , p. 1.
D. Leborgne, Calculus differenziale et géometry , Puf, 1982 ( ISBN 2130374956 ) , p. 16
Questo aneddoto viene da Hatcher 2001 , p. 32.
(in) Jiri Matousek , Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry , Springer,2003, 196 p. ( ISBN 978-3-540-00362-5 , leggi online ) , p. 47
Questo risultato è una conseguenza del teorema di Borsuk-Ulam ( Hatcher 2001 , p. 33).