Conduzione termica
La conduzione del calore (o diffusione termica ) è una modalità di trasferimento del calore causata da una differenza di temperatura tra due aree di uno stesso mezzo o tra due mezzi a contatto, e senza eseguire lo spostamento complessivo del materiale (scala macroscopica ) rispetto alla convezione che è un'altra modalità di trasferimento del calore . Può essere interpretata come la trasmissione graduale dell'agitazione termica : un atomo (o una molecola) cede parte della sua energia cinetica all'atomo vicino.
La conduzione termica è un processo di trasporto dell'energia interna legato all'agitazione molecolare e dovuto ad un'eterogeneità del mezzo su scala macroscopica. È un fenomeno irreversibile analogo al fenomeno della diffusione . Nei fluidi (liquidi e gas) questo trasporto di energia risulta a livello microscopico dall'anisotropia della funzione di distribuzione della velocità . Nei solidi, la conduzione termica è fornita congiuntamente dagli elettroni di conduzione e dalle vibrazioni del reticolo cristallino ( fononi ).
Fenomeni fisici
La conduzione termica è il movimento dell'energia termica dalle parti calde di un impianto a quelle fredde. Man mano che l'energia si diffonde attraverso un sistema, le differenze di temperatura diminuiscono e l' entropia aumenta.
Nel caso più semplice dei gas, la diffusione dell'energia termica avviene quando, durante il suo movimento di traslazione, una particella cede parte della sua quantità di moto ad altre particelle durante le collisioni.
Nei solidi, il movimento di traslazione assume la forma di fononi (vedi figura). I fononi sono quantità elementari (quantizzate) di energia vibratoria che si muovono attraverso un solido alla velocità del suono specifica della sostanza. Il modo in cui i fononi interagiscono nel solido determina le loro proprietà, come la diffusione termica. Gli isolanti elettrici, ad esempio, hanno generalmente una bassa conduttività termica e questi solidi sono considerati isolanti termici (come vetro, plastica, gomma, ceramica e pietra). Questo perché nei solidi gli atomi e le molecole non sono liberi di muoversi.
Il metallo , invece, ha un'elevata conducibilità termica. La loro struttura infatti consente la diffusione dell'energia cinetica da parte di elettroni di conduzione , leggeri ed estremamente mobili. Questo è il motivo per cui nei metalli c'è una correlazione quasi perfetta tra conducibilità elettrica e conducibilità termica . La conduttività elettronica predomina nei metalli perché gli elettroni sono delocalizzati , cioè non sono legati a un atomo e si comportano come un gas quantistico.
Informazioni generali sulla modellazione
Legge di Fourier
La conduzione termica è un trasferimento di calore spontaneo da una regione di alta temperatura a una regione di temperatura inferiore, ed è descritta dalla cosiddetta legge di Fourier stabilita matematicamente da Jean-Baptiste Biot nel 1804 e poi sperimentalmente da Fourier nel 1822 : densità del calore la portata è proporzionale al gradiente di temperatura.
La costante di proporzionalità λ è chiamata conducibilità termica del materiale. È sempre positiva.
Con le unità del Sistema Internazionale, la conducibilità termica λ è espressa in watt per metro-Kelvin ( W m −1 K −1 ). La densità del flusso di calore è espressa in watt per metro quadrato ( W m −2 ), la temperatura T , in kelvin ( K ).
La legge di Fourier è una legge macroscopica. È valido solo per solidi di grandi dimensioni rispetto al cammino libero medio e alla lunghezza d' onda dei fononi coinvolti nei trasferimenti di calore.
La legge di Fourier è una legge fenomenologica analoga alla legge di Fick per la diffusione delle particelle o alla legge di Ohm per la conduzione elettrica (Ohm usò anche un'analogia tra termica ed elettricità per costruire la sua teoria). Queste tre leggi possono essere interpretate allo stesso modo: la disomogeneità di un parametro intensivo (temperatura, numero di particelle per unità di volume, potenziale elettrico ) provoca un fenomeno di trasporto tendente a compensare lo squilibrio (flusso di calore, corrente di diffusione, attuale).
Complemento
Possiamo esprimere il trasferimento di calore secondo Ox per un tempo dt . Si assume che la quantità di calore che passa attraverso una superficie di area dS x sia proporzionale a dS x , al tempo di trasferimento dt e alla velocità di variazione della temperatura T :
La densità del flusso termico attraverso la superficie elementare dS x è quindi:
Possiamo dedurre la densità del flusso nella direzione del Bue:
Lo stesso ragionamento in ciascuna delle direzioni dello spazio fornisce la legge di Fourier.
Equazione del calore
Un bilancio energetico e l'espressione della legge di Fourier porta all'equazione generale della conduzione del calore in un corpo omogeneo, equazione del trasporto della temperatura :
o
| è la conducibilità termica del materiale in W m −1 K −1 , | |
| è l'energia prodotta all'interno del materiale stesso in W m −3 , | |
| è la densità in kg / m 3 | |
| è la massa termica specifica del materiale in J kg −1 K −1 . |
In forma unidimensionale e nel caso in cui P è zero e la conducibilità è costante, si ottiene:
In regime stazionario, quando la temperatura non cambia più nel tempo e se P è zero, si riduce a: che è un'equazione di Laplace . T è quindi una funzione armonica .
Nel caso di regime permanente e unidimensionale, l'equazione precedente è ridotta a: la cui soluzione è T = Ax + b dove A e B sono costanti da fissare secondo le condizioni al contorno.
Scala microscopica: l'equazione di Boltzmann-Peierls
In problemi a scala nanometrica come riscontriamo ad esempio nella microelettronica, il cammino libero medio dei fononi non è piccolo rispetto alla dimensione dell'oggetto studiato e l'equazione di diffusione del calore non è più valida. Questo problema fu risolto da Rudolf Peierls nel 1929 fornendo una descrizione microscopica del fenomeno mediante un'equazione di Boltzmann per l'energia d E ν trasferita dai fononi considerati gas, come il gas dei fotoni . Questa energia è ridotta all'unità di area attraversata d S , all'intervallo di frequenza considerato dν , all'angolo solido elementare considerato dΩ e all'intervallo di tempo d t per dare un'intensità I ν
Questa quantità è l'analogo della luminanza spettrale per la radiazione. Obbedisce all'equazione di Boltzmann che diamo qui in una dimensione spaziale e nel caso stazionario
Per questo :
- abbiamo introdotto la quantità τ = κ x ; dove κ è il coefficiente di assorbimento spettrale del mezzo che si presume sia indipendente da ν . Questa quantità è l'inverso del cammino libero medio l = 1 / τ , tipicamente poche decine di nm a temperatura ambiente;
- si è ipotizzato che la dipendenza angolare fosse di rivoluzione, caratterizzata da μ = cos θ ;
- i termini di diffusione che possono derivare da difetti di cristallo o processi di umklapp sono stati trascurati .
G ν è il termine di creazione che risulta dalla creazione di fononi mediante agitazione termica.
Nel caso in cui si raggiunga l'equilibrio termodinamico questo termine è dato dalla legge di Planck (i fononi sono bosoni proprio come i fotoni, quindi obbediscono alla statistica di Bose-Einstein )
o
| T m | temperatura di vibrazione unica per tutti i gradi di libertà del reticolo cristallino di dilatazione, torsione, flessione), |
| h | Costante di Planck , |
| K | Costante di Boltzmann , |
| σ | Costante di Stefan-Boltzmann , |
| c m | velocità del gruppo per la propagazione (tipicamente poche migliaia di m / s). È la media delle velocità longitudinale e trasversale, a volte chiamata velocità di Debye . |
Partendo dall'assunzione dell'equilibrio termodinamico del mezzo si può scrivere un'equazione dell'intensità identica a quella del trasferimento radiativo . Otteniamo un'equazione per l'intensità integrata in frequenza :
Collegamento con la scala macroscopica
Introduciamo i primi momenti di I m :
| - energia | |
| - la densità del flusso di calore |
dove ρ è la densità e C V è la capacità termica specifica .
Quando :
- il percorso libero medio è piccolo rispetto alla dimensione del dominio o qualsiasi altra quantità che caratterizza la soluzione, vale a dire ,
- il tempo caratteristico è piccolo rispetto a qualsiasi variazione temporale nel dominio ,
vari metodi consentono di ottenere un'equazione di diffusione correlando queste grandezze nella forma:
Riconosciamo la legge di Fourier con una conducibilità termica di
DimostrazioneCome nel trasferimento radiativo , possiamo ridurre l'equazione di Boltzmann al seguente sistema
Supponiamo che il tensore isotropo : sia il metodo di Eddington o il metodo P 1 .
Quindi otteniamo
Assumendo una densità di flusso costante, viene scritta la seconda equazione del sistema precedente
La conducibilità termica è proporzionale alla velocità di propagazione, alla capacità termica specifica e al percorso libero medio nel mezzo.
Di conseguenza, il coefficiente di diffusione termica è proporzionale alla velocità di propagazione e al cammino libero medio.
L'equazione del calore ottenuta con questa approssimazione diffusiva è un'equazione parabolica per la quale la velocità di propagazione dell'informazione è infinita.
Scale temporali brevi: l'equazione di Cattaneo-Vernotte
In alcuni casi l'ipotesi di quasi-stazionarietà del flusso non è più valida: ad esempio se per riscaldare un campione si utilizza una sorgente di calore ultracorta come un impulso laser.
Se manteniamo il termine temporale sul flusso (vedi box precedente) otteniamo:
Questa espressione del flusso che include un termine di rilassamento per l'oscillazione dei fononi è chiamata equazione di Cattaneo-Vernotte da Carlo Cattaneo e Pierre Vernotte. Il sistema a cui conduce è del tipo delle equazioni degli operatori telegrafici . Si noti che in questo sistema di equazioni alle derivate parziali iperboliche la velocità di propagazione dell'informazione è c m / √ 3 e non c m .
Scala nanoscopica: il quanto di calore
Consideriamo una guida d' onda virtuale di dimensioni nanoscopiche. Rolf Landauer ha dimostrato che il flusso di calore per il modo di propagazione α tra un mezzo 1 e un mezzo 2 all'equilibrio termodinamico è
o
| numero d'onda ; | |
| relazione di dispersione ; | |
| numero di occupazione della statistica di Bose-Einstein ; | |
| fattore di trasmissione. |
La guida è limitato da due superfici di scambio perfetto: . Alle sue estremità applichiamo due media con una differenza di temperatura e consideriamo il limite . Si presume che queste temperature siano sufficientemente basse da avere il diritto di prendere in considerazione solo il numero d'onda k = 0 per ciascuna modalità.
Con questi presupposti abbiamo dimostrato che la conduttanza quantistica per ogni modalità è
Questo valore è stato misurato sperimentalmente.
Conduzione allo stato stazionario
Uno stato stazionario è definito dall'indipendenza dal tempo di qualsiasi quantità, inclusa la temperatura.
Nota: lo stato stazionario a volte viene confuso con lo stato stazionario , mentre uno stato stazionario può dipendere dal tempo (esempio: un regime periodico).
Superficie piana semplice
Il materiale è un mezzo delimitato da due piani paralleli (caso di un muro). Ogni piano ha una temperatura T omogenea su tutta la sua superficie. Si ritiene che i piani abbiano dimensioni infinite per essere privi di effetti di bordo. Di conseguenza, il mezzo è unidimensionale e la densità del flusso è la stessa in tutti i punti. Si presume inoltre che la conduttività sia costante.
Indichiamo con T 1 la temperatura del piano posto all'ascissa x 1 e T 2 la temperatura del piano situato all'ascissa x 2 . Indichiamo con e = x 2 - x 1 lo spessore del muro. Nello stato stazionario, T è una funzione affine di x , quindi:
La densità del flusso termico superficiale è scritta:
Il flusso termico attraverso una superficie S vale:
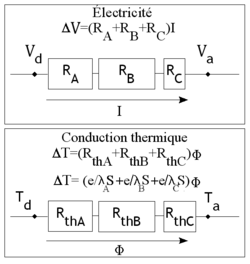
Analogia elettrica
Per analogia con l' elettricità ( legge di Ohm ) possiamo mettere in parallelo le due espressioni:
Possiamo mettere in parallelo da un lato la tensione e la temperatura, dall'altro l'intensità e il flusso di calore:
Possiamo quindi definire una resistenza termica , giocando nel trasferimento di calore un ruolo paragonabile alla resistenza elettrica.
dove S è la superficie del materiale ed e il suo spessore. La resistenza termica R thc è omogenea a K W −1
Superfici piane in serie

Consideriamo materiali A , B e C con rispettivi spessori all'e A , e B e e C e rispettive conduttività lambda A , λ B e λ C .
Le ipotesi sono le stesse di una semplice superficie piana. Si ritiene che il contatto tra ogni strato sia perfetto, il che significa che la temperatura all'interfaccia tra 2 materiali è identica in ogni materiale (nessun salto di temperatura quando si passa un'interfaccia).
Le resistenze termiche si sommano:
DimostrazioneNel complesso abbiamo
Se ci decomponiamo
Per lo strato A : per lo strato B : per lo strato C :Nota: presumendo che il flusso (o la densità di flusso) sia costante.
Con:
pertanto
Profilo di temperaturaPer ogni materiale la variazione di temperatura segue una legge del tipo:
La variazione di temperatura è quindi lineare nello spessore del materiale considerato. La pendenza dipende dalla caratteristica λ ( conducibilità termica ) di ciascun materiale. Più bassa è la conducibilità termica (e quindi più isolante è il materiale), più ripida sarà la pendenza.
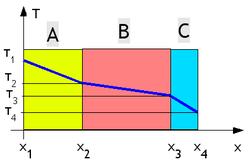 Analogia elettrica
Analogia elettricaAllo stesso modo in cui si sommano le resistenze elettriche in serie, si sommano le resistenze termiche in serie.
Superfici piane in parallelo

Consideriamo materiali piani giustapposti. Ogni materiale è omogeneo e limitato da due piani paralleli. Questo è ad esempio il caso di un muro con una finestra.
Le ipotesi sono le stesse di una semplice superficie piana. Inoltre, si considera che la temperatura sia uniforme sulla superficie di ogni elemento (T 1 e T 2 ).
Siano S A , S B e S C le rispettive superfici degli elementi A, B e C.
Successivamente, assumiamo che il flusso sia sempre perpendicolare alla parete del composto; ciò non è realistico in quanto la temperatura superficiale di ogni elemento che lo compone è diversa e di conseguenza si ha un gradiente termico laterale (all'origine dei ponti termici). Inoltre, è necessario correggere il flusso di calore calcolato nella parete composita utilizzando coefficienti di perdita lineare, specifici per ogni giunzione di parete (e che possono essere trascurabili, vedi regolazione termica TH 2000).
Le conduttanze termiche si sommano:
DimostrazionePer ogni elemento, il flusso è espresso in base alla relazione
Con prendendo l'analogia elettrica
dove è uguale a , o Abbiamo quindi
Il flusso totale è uguale alla somma dei flussi in ogni elemento
Sia S l'area totale
Il flusso superficiale viene quindi scritto
Sempre per analogia con le leggi elettriche, l'inverso della resistenza termica è talvolta chiamato conduttanza termica.
Analogia elettricaÈ quindi possibile anche fare un'analogia tra un collegamento elettrico di resistenze in parallelo.

|

|
Superficie cilindrica semplice
Il singolo tubo è costituito da un unico materiale omogeneo. La temperatura è omogenea su ogni superficie del tubo. Si considera che il tubo abbia una lunghezza infinita per essere esente da effetti di bordo.
La variazione di temperatura è scritta:
DimostrazioneSe consideriamo una variazione dR all'interno del materiale costituente il tubo, la legge di Fourier viene quindi espressa:
(l'ipotesi di stato stazionario infatti fa sì che il flusso di calore sia costante nel bollitore ed è quindi indipendente dalla posizione scelta)
Variazione della temperatura nello spessore del tuboSia S la superficie di un cilindro:
Possiamo scrivere la legge di Fourier nella forma:
La variazione di temperatura nel materiale è quindi
Su tutto lo spessore del tubo, la variazione è
Superfici cilindriche concentriche
Il tubo concentrico è costituito da tubi disposti in strati concentrici. Si considera che il contatto tra i tubi sia perfetto. La temperatura è omogenea su ogni superficie del tubo. Si considera che il tubo abbia una lunghezza L infinita per essere esente da effetti di bordo.
La resistenza totale del tubo è espressa secondo una legge di tipo “serie” come la parete composta da serie:
DimostrazioneEvoluzione della temperatura nel primo strato:
Evoluzione della temperatura nel secondo strato:
Su tutto lo spessore del tubo:
La resistenza termica dello strato A
La resistenza termica dello strato B
La resistenza totale del tubo è espressa secondo una legge di tipo “serie” come la parete composta da serie:
Conduzione in regime dinamico
La risoluzione dell'equazione del calore in regime dinamico è molto più delicata. Utilizza i concetti di trasformata di Fourier , prodotto di convoluzione e distribuzioni . Diamo alcuni esempi di risoluzione.
Caso di un dominio illimitato
Principio generaleScriviamo l'equazione del calore nella forma:
dove D è il coefficiente di diffusività termica e P qui rappresenta il riscaldamento (in K / s) da fonti di calore. P può essere una funzione del tempo e della posizione della fonte di calore, ma anche una distribuzione . Ad esempio, l'iniezione istantanea e puntuale di una quantità di calore può essere rappresentata dal prodotto di una distribuzione di Dirac al tempo t = 0 per una distribuzione di Dirac in x = 0, essendo x l'ascissa nel caso di un problema unidimensionale o il vettore di posizione nel caso generale.
Diamo anche a noi stessi lo stato iniziale del dominio , che può anche essere una funzione di x o una distribuzione.
Il metodo di risoluzione consiste in:
- applicare una trasformata di Fourier relativa alla variabile x, a tutti i termini dell'equazione differenziale. Questo trasforma la derivazione rispetto a x da un prodotto. Se prendiamo , l'equazione diventa:
- riconoscere in questa equazione un prodotto di convoluzione :
- applicare il reciproco dell'operatore il cui valore è mostrato , dove H è la funzione Heaviside , per finire con:
Se F ( P ) è una funzione e non una distribuzione, questa relazione diventa, per t > 0:
- prendendo la trasformata di Fourier inversa per ricavare T .
Se prendiamo e (iniezione istantanea di calore in un dato punto), il metodo sopra descritto porta a:
quindi, per t> 0:
la cui trasformata di Fourier inversa è, per t> 0:
nel caso unidimensionale; nel caso tridimensionale. Dominio illimitato senza fonte di caloreSe ci diamo solo la temperatura iniziale del mezzo senza una fonte di calore (P = 0), allora troviamo che:
nel caso unidimensionale. nel caso tridimensionale.Caso di aree limitate, senza fonte di calore
Caso di un dominio limitato da un piano. Il problema di KelvinSupponiamo che il dominio limitato dal piano x = 0. Se ci diamo come condizione al contorno aggiuntiva T (0, t) = 0 per ogni t, allora, è sufficiente estendere la distribuzione della temperatura iniziale di una funzione dispari in x e applicare il risultato precedente.
Il caso più famoso è quello del problema Kelvin . Quest'ultimo negli anni '60 dell'Ottocento considerava che la Terra si trovava inizialmente a una temperatura costante dell'ordine di 3000 ° C e che si raffreddava per semplice conduzione. Usando il valore attuale del gradiente di temperatura in funzione della profondità, ha ricavato una stima dell'età della Terra . Possiamo applicare il metodo di risoluzione precedente considerando la Terra come piatta e infinitamente profonda, limitata dal piano della sua superficie. Il calcolo porta a:
dove si dice che erf sia la funzione di errore gaussiano .
Il gradiente di temperatura in superficie è:
:Conoscendo circa 3 ° C per 100 metri di profondità e D stimata in 10 −6 m 2 s −1 , troviamo che vale 100 milioni di anni. Questo risultato è ampiamente sottovalutato perché Kelvin ha ignorato i fenomeni di convezione all'interno del mantello terrestre .
Caso di un dominio delimitato da due piani paralleliConsidera un dominio limitato dai due piani x = 0 ex = L. Supponiamo di darci come condizioni al contorno T (0, t) = T (L, t) = 0. Usiamo un metodo di risoluzione basato sulla serie di Fourier , cercando T nella forma:
Questa espressione controlla sia l'equazione del calore che le condizioni al contorno. Se ci diamo la distribuzione della temperatura iniziale , è sufficiente svilupparla in serie di Fourier per determinarli .
Ad esempio, se prendiamo costante, otteniamo:
Facendo tendere L all'infinito, troviamo la soluzione di Kelvin del paragrafo precedente , considerando la somma precedente come una somma di Riemann convergente all'integrale.
Caso di un dominio con geometria sfericaNel caso in cui la propagazione avvenga in un dominio sferico, e dove la temperatura dipenda solo dalla distanza r al centro, l'equazione del calore diventa, tenendo conto dell'espressione del laplaciano in sferica :
Se ci mettiamo in posa , l'equazione diventa:
Possiamo quindi applicare i metodi precedenti per determinare F, quindi dedurre T dividendo per r .
Pertanto, la risoluzione del problema di Kelvin nel caso di una sfera di raggio R (temperatura iniziale uniformemente uguale a , la superficie essendo mantenuta a temperatura zero) porta alla seguente espressione di T:
dove sinc è la funzione seno cardinale .
Caso di aree limitate, con fonte di calore
Consideriamo l'equazione:
con P non zero. Generalmente cerchiamo una soluzione particolare a questa equazione, in modo che, una volta sottratta da T, possiamo ridurci a un'equazione senza un secondo membro. Ecco alcuni esempi, nel caso in cui P rappresenta una densità di fonte di calore costante, indipendente dalla posizione e dal tempo.
Dominio delimitato da due piani paralleliConsidera un dominio limitato dai due piani x = 0 ex = L. Si suppone che al momento iniziale la temperatura del campo sia uguale a una temperatura di riferimento zero e che i bordi del campo rimangano permanentemente a questa temperatura zero. T quindi verifica:
T (0, t ) = T (L, t ) = 0 per ogni t positivo. T ( x , 0) = 0 per tutte le x comprese tra 0 e L.La funzione indipendente di t soddisfa le prime due relazioni, così che, se poniamo , allora G soddisfa:
Possiamo applicare il metodo visto sopra cercando G sotto forma di una serie:
che controlla le prime due relazioni. Poiché, per ragioni di simmetria, ci aspettiamo che , possiamo supporre che i coefficienti siano zero quando n è pari, così che:
:Per t = 0, abbiamo:
:Li troviamo sviluppando nella serie di Fourier . Noi troviamo :
Quindi G, quindi finalmente:
Quando t tende verso l'infinito, la temperatura del dominio tende verso , il riscaldamento termico nel mezzo essendo quindi in equilibrio con l'evacuazione del calore dai due bordi.
Dominio limitato da un pianoLa risoluzione dello stesso problema nel caso in cui x > 0 consiste nel determinare T tale che:
T (0, t ) = 0 per ogni t positivo. T ( x , 0) = 0 per ogni x > 0.Possiamo ottenere la soluzione facendo tendere L verso l'infinito nell'espressione data nel paragrafo precedente , assimilando la serie ad una somma di Riemann . Otteniamo quindi la seguente espressione:
erf è la funzione nota come funzione di errore gaussiano . Possiamo trovare questa espressione anche applicando il metodo risultante dal principio generale relativo a un dominio illimitato, dopo aver esteso a tutto lo spazio le funzioni T e P nelle funzioni dispari in x , così che T svanisce in x = 0.
Quando t tende all'infinito, T è uguale a circa P t , analogo a quello di un dominio infinito. L'unico bordo non è sufficiente per dissipare il calore.
Dominio della geometria sfericaNel caso di un dominio il cui bordo è una sfera di raggio R, si usa l'espressione del laplaciano in sferica e si viene portati a risolvere:
Per ogni t , T (R, t ) = 0 Per ogni r , T ( r , 0) = 0Posando , G verifica il sistema:
Per ogni t , G (R, t ) = 0 Per tutte le R ,Il metodo della serie di Fourier suggerisce di cercare G sotto forma di una serie , dove si trovano espandendosi in una serie di Fourier. Otteniamo :
:e così :
dove sinc è la funzione seno cardinale .
Quando t tende all'infinito, la temperatura T tende verso la distribuzione limite .
Note e riferimenti
Appunti
- Il termine sistema designa un corpo o un insieme di corpi in cui avvengono gli scambi di calore.
- Il diamante è una notevole eccezione: il suo reticolo cristallino rigido ha molti modi di vibrazione quantizzati. Di conseguenza, il diamante ha sia una capacità termica molto bassa che un'elevata conduttività termica .
- Spesso è zero (caso di depositi di calore sulla superficie dei muri, per esempio), ma possiamo citare molti casi in cui non lo è; includere tra l'altro lo studio del trasferimento di calore per conduzione all'interno del combustibile nucleare, o l'assorbimento di luce o microonde in materiali semitrasparenti, ecc.
- La convezione portando materiali caldi in prossimità della superficie, il gradiente di temperatura in prossimità di questi ultimi dopo un dato tempo è maggiore nel caso di convezione che in quello di conduzione. Di conseguenza, il tempo di raffreddamento che porta ad un dato gradiente sarà stimato essere più breve nel caso di conduzione che in quello di convezione. Vedi England P, Molnar P, Richter F, Kelvin, Perry and the Age of the Earth , Pour la Science , febbraio 2008, p. 32-37 , tradotto da un articolo di American Scientist . Una seconda e più marginale fonte di errore deriva dal fatto che Kelvin trascura anche il termine fonte di energia a causa della radioattività.
Riferimenti
- José-Philippe Pérez e AM Romulus, Termodinamica. Fondamenti e applicazioni , Parigi, Masson ,1993, p. 153.
- Pérez e Romolo 1993 , pag. 158
- Pérez e Romulus 1993 , p. 160
- Vedi Wiedemann e Franz Law .
- Joseph Fourier , Teoria analitica del calore ,1822[ dettaglio delle edizioni ], Edward Leroy, " Sull'integrazione delle equazioni del calore " Asens , 3 serie E , t. 14,1897, p. 379-465 ( leggi in linea )e link esterni ( vedi sotto ).
- Flussi di calore che sfuggono a Fourier, Pour la Science n o 494 dicembre 2018 p. 63 .
- (in) Yuan Dong Dynamical Analysis of Non-Fourier Heat Conduction in Nanosystems , Springer ,2016( leggi online )
- O. Bourgeois, D. Tainoff, N. Mingo, B. Vermeersch e J.-L. Barrat, " Des fluxes de solidarité which escape Fourier ", Pour la Science , n . 494,2008, p. 58-65.
- (De) RE Peierls , " Zur kinetischen Theorie der Wärmeleitung in Kristallen " , Annalen der Physik , vol. 3,1929, p. 1055–1101
- (in) Ingo Müller e Tommaso Ruggeri, Rational Extended Thermodynamics , vol. 37, Springer , coll. "Springer Tracts in Natural Philosophy",1998( ISBN 978-1-4612-7460-5 )
- () Michael M. Modest , Radiative Heat Transfer , Academic Press ,2003( ISBN 0-12-503163-7 )
- (it) Carlo Cattaneo , " Sulla Conduzione del Calore " , Atti del Seminario Matematico e Fisico dell 'Universita di Modena e Reggio Emilia , vol. 3,1948, p. 83–101
- P. Vernotte, " I paradossi della teoria continua dell'equazione del calore ", Atti dell'Accademia delle Scienze , vol. 246, 1958 1958, pag. 3154-3155
- (a) Yoseph Imry, Introduzione alla fisica mesoscopica , Oxford University Press ,2002( ISBN 0-19-850738-0 , leggi online )
- (in) JB Pendry , " Quantum Limits to the Flow of Information and Entropy " , Journal of Physics A: Mathematical and General , vol. 16, n o 10,1983, p. 2161-2171 ( leggi in linea )
- (a) K. Schwab, EA Enriksen, JM Worlock e ML Roukes, " Measurement of the Quantum of Thermal Conductance " , Letters to Nature , vol. 404,2000, p. 974-977 ( leggi in linea )
- Lev Landau e Evgueni Lifchits , Theoretical Physics , t. 6: Meccanica dei fluidi [ dettaglio delle edizioni ].
- Laurent Schwartz , Metodi matematici per le scienze fisiche , Hermann , 1965.
- Jean-Louis Le Mouel, il raffreddamento della Terra , 196 ° Conferenza dell'Università di ogni conoscenza, 14 luglio 2000 [1] o [2]
- John Perry, On the age of earth , 51 , Nature (7 febbraio 1895), 341-342
Vedi anche
Articoli Correlati
- Diffusività termica
- Diffusione della materia
- Conduttività termica
- Trasferimento termico
- Conduttanza elettrica
- Omogeneizzazione
- Termodinamica del non equilibrio
- Fluttuazioni termodinamiche
link esterno
- corso di base essenziale http://www.ryounes.net/cours/conduction.pdf
- corso di base completo: http://www.sciences.univ-nantes.fr/sites/claude_saintblanquet/index.htm
- http://www.lmm.jussieu.fr/~lagree/COURS/MECAVENIR







![{\displaystyle {\vec {\nabla }}\cdot \left[\lambda (T)\,{\vec {\nabla }}T\right]+{\mathcal {P}}({\vec {r}})=\rho \,C_{P}(T)\,{\frac {\partial T}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a34ba437fd805ac3d4aa2e6d2edfd587f79214e)



















![{\displaystyle {\begin{array}{rcl}{\frac {\partial E_{m}}{\partial t}}+{\frac {\partial \mathbf {\varphi } _{m}}{\partial x}}&=&\kappa \left(4\pi B_{m}-c_{m}E_{m}\right)\\[0.6em]{\frac {\partial \mathbf {\varphi } _{m}}{\partial t}}+c_{m}^{2}{\frac {\partial \mathbf {(} E_{m}{\mathsf {D}}_{m})}{\partial x}}&=&-c_{m}\kappa \mathbf {\varphi } _{m}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/002d75e8b41baae61ec211e85b9b205088d56178)





















































































































