Legge dello studente

t legge dello studente
Densità di probabilità


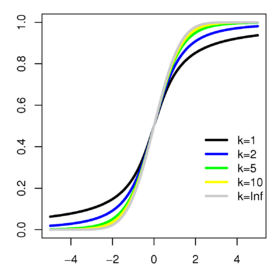Funzione di distribuzione

impostazioni	k > 0 (gradi di libertà)
Supporto	$x \ in \ mathbb {R}$
Densità di probabilità	$f_ {T} (t) = {\ frac {1} {{\ sqrt {k \ pi}}}} {\ frac {\ Gamma ({\ frac {k + 1} {2}})} {\ Gamma ({\ frac {k} {2}})}} \ sinistra (1 + {\ frac {t ^ {2}} {k}} \ destra) ^ {{- {\ frac {k + 1} {2 }}}}$
Funzione di distribuzione	${\ displaystyle {\ begin {matrix} {\ frac {1} {2}} + x \ Gamma \ left ({\ frac {k + 1} {2}} \ right) {\ frac {\, _ {2 } F_ {1} \ sinistra ({\ frac {1} {2}}, {\ frac {k + 1} {2}}; {\ frac {3} {2}}; - {\ frac {x ^ {2}} {k}} \ destra)} {{\ sqrt {k \ pi}} \, \ Gamma \ sinistra ({\ frac {k} {2}} \ destra)}} \ fine {matrice}} }$ dove 2 F 1 è la funzione ipergeometrica
Speranza	se k ≤ 1: forma indeterminata se k > 1: 0
Mediano	0
Moda	0
Varianza	se k ≤ 1: forma indeterminata se 1 < k ≤ 2: + ∞ se k > 2: ${\ frac {k} {k-2}}$
Asimmetria	se k ≤ 3: forma indeterminata se k > 3: 0
Kurtosi normalizzata	se k ≤ 2: forma indeterminata se 2 < k ≤ 4: + ∞ se k > 4: ${\ frac {6} {k-4}}$

In teoria delle probabilità e statistiche , la legge di Student è una legge di probabilità , coinvolgendo il quoziente tra una variabile a seguito di una ridotta centrata legge normale e la radice quadrata di una variabile distribuita secondo il diritto di $χ 2$ .

Viene utilizzato in particolare per i test di Student , la costruzione dell'intervallo di confidenza e l'inferenza bayesiana .

Definizione e proprietà

Lasciare $Z sia$ una variabile casuale con un centrato e ridotta distribuzione normale e lasciare $U tramite$ una variabile indipendente di $Z$ e distribuiti secondo la legge del $χ 2$ con $k$ gradi di libertà. Per definizione, la variabile

T = {\ frac {Z} {{\ sqrt {U / k}}}}

segue una legge di Student con $k$ gradi di libertà.

{\ displaystyle U = \ sum _ {i = 1} ^ {k} X_ {i} ^ {2}}

, allora , dove le

X

i

sono

k

variabili casuali reali iid di distribuzione normale centrata-ridotta .

{\ displaystyle U \ sim \ chi _ {k} ^ {2}}

La densità di $T$ , indicata con $f T$ , è data da:

{\ displaystyle f_ {T} (t) = {\ frac {1} {\ sqrt {k \ pi}}} {\ frac {\ Gamma ({\ frac {k + 1} {2}})} {\ Gamma ({\ frac {k} {2}})}} \ sinistra (1 + {\ frac {t ^ {2}} {k}} \ destra) ^ {- {\ frac {k + 1} {2 }}}, \; {\ textrm {per}} \; k> 0}

dove $Γ$ è la funzione Gamma di Eulero .

La densità $f T$ associata alla variabile $T$ è simmetrica, centrata in 0 e a campana.

La sua aspettativa non può essere definita per $k = 1$ ed è zero per $k > 1$ .

La sua varianza è infinita per $k = 2$ ed è uguale a $K / k - 2$ per $k > 2$ .

Limita il comportamento

Quando $k$ è grande, la legge di Student può essere approssimata dalla legge normale centrata ridotta . Un modo semplice per dimostrarlo è usare il lemma di Scheffé .

Storia

Il calcolo della legge dello studente è stato descritto nel 1908 da William Gosset mentre era impiegato presso la fabbrica di birra Guinness a Dublino. Il suo capo, presumibilmente per motivi di concorrenza, ha proibito ai suoi dipendenti di pubblicare con il proprio nome. Per questo Gosset sceglie uno pseudonimo, Student , che in inglese significa studente. Il t- test e la teoria divennero famosi grazie all'opera di Ronald Fisher che diede alla legge il nome di “Legge dello studente”.

Legge dello studente nel campionamento

Siano $X 1 , ..., X n$ , $n$ variabili mutuamente indipendenti distribuite secondo la stessa legge normale di aspettativa $μ$ e di varianza $σ$ $2$ che corrispondono a un campione di dimensione $n$ . Considera la media empirica ${\ displaystyle {\ mathcal {N}} (\ mu, \ sigma ^ {2})}$

{\ displaystyle {\ overline {X}} = {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} X_ {i}}

e lo stimatore imparziale della varianza

{\ displaystyle S ^ {2} = {\ frac {1} {n-1}} \ sum _ {i = 1} ^ {n} (X_ {i} - {\ overline {X}}) ^ {2 }}

Per normalizzazione, la variabile casuale

{\ displaystyle Z = {\ frac {{\ overline {X}} - \ mu} {\ sigma / {\ sqrt {n}}}}}

segue una distribuzione normale standard (aspettativa 0 e varianza 1). La variabile casuale ottenuto sostituendo $σ$ da $S$ in IS $Z$

{\ displaystyle T = {\ frac {{\ overline {X}} - \ mu} {S / {\ sqrt {n}}}}}

$T$ segue la legge di Student a $n - 1$ gradi di libertà. Questo risultato è utile per trovare gli intervalli di confidenza quando $σ 2$ è sconosciuto, come illustrato di seguito.

Per giustificare ciò, introduciamo la variabile casuale

{\ displaystyle U = {\ frac {1} {\ sigma ^ {2}}} \ sum _ {i = 1} ^ {n} (X_ {i} - {\ overline {X}}) ^ {2} }

che permette di scrivere e ${\ displaystyle {\ frac {S ^ {2}} {\ sigma ^ {2}}} = {\ frac {U} {n-1}}}$

{\ displaystyle T = {\ frac {{\ overline {X}} - \ mu} {\ sigma / {\ sqrt {n}}}} {\ frac {1} {S / \ sigma}} = {\ frac {Z} {\ sqrt {U / (n-1)}}}}

Per finire è necessario dimostrare che $Z$ e $U$ sono indipendenti e che $U$ segue una legge del $\times 2$ con $n - 1$ gradi di libertà.

Si noti la perdita di un grado di libertà perché anche se ci sono $n$ variabili casuali indipendenti $X i$ , non lo sono poiché la loro somma è 0. ${\ displaystyle X_ {i} - {\ overline {X}}}$

Applicazione: intervallo di confidenza associato all'aspettativa di una variabile di distribuzione normale di varianza sconosciuta

Questo capitolo presenta un metodo per determinare l' intervallo di confidenza dell'aspettativa $μ$ di una distribuzione normale . Nota che se la varianza è nota, è meglio usare la distribuzione normale direttamente con la media . $\ sopra {X}$

Teorema - Dato un rischio compreso tra 0 e 1, abbiamo $\alfa$

{\ displaystyle \ mathbb {P} \ left (-t _ {\ alpha / 2} ^ {n-1} <{\ frac {{\ overline {X}} - \ mu} {S / {\ sqrt {n } }}} <t _ {\ alpha / 2} ^ {n-1} \ destra) = 1- \ alpha}

L'intervallo di confidenza a due code di $μ$ al livello di confidenza è dato da: ${\ displaystyle 1- \ alfa}$

{\ displaystyle \ left [\, {\ overline {X}} - t _ {\ alpha / 2} ^ {n-1} {\ tfrac {S} {\ sqrt {n}}}; {\ overline {X } } + t _ {\ alpha / 2} ^ {n-1} {\ tfrac {S} {\ sqrt {n}}} \, \ destra]}

con , lo stimatore puntuale dell'aspettativa e , lo stimatore imparziale della varianza definita sopra. $\ sopra {X}$ $S$

$t _ {{\ gamma}} ^ {{k}}$ è il quantile d' ordine della legge di Student con k gradi di libertà, è il numero unico che soddisfa ${\ displaystyle 1- \ gamma}$

{\ displaystyle \ mathbb {P} (T \ leq t _ {\ gamma} ^ {k}) = 1- \ gamma}

quando $T$ segue la legge di Student con $k$ gradi di libertà.

Dimostrazione

Mettiamoci di nuovo in posa

{\ displaystyle T = {\ frac {{\ overline {X}} - \ mu} {S / {\ sqrt {n}}}}}

Abbiamo visto che $T$ segue una legge di Student con $n$ -1 gradi di libertà. Con la simmetria e la continuità della legge abbiamo

{\ displaystyle \ mathbb {P} (-t \ leq T \ leq t) = \ mathbb {P} (T \ leq t) - \ mathbb {P} (T <-t) = \ mathbb {P} (T \ leq t) - \ mathbb {P} (T> t) = 2 \ mathbb {P} (T \ leq t) -1}

In particolare

{\ displaystyle \ mathbb {P} (-t _ {\ alpha / 2} ^ {k} \ leq T \ leq t _ {\ alpha} ^ {k}) = 2 (1- \ alpha / 2) -1 = 1 - \ alfa}

questo dà la probabilità cercata. L'intervallo è dato da

{\ displaystyle -t _ {\ alpha / 2} ^ {n-1} \ leq {\ frac {{\ overline {X}} - \ mu} {S / {\ sqrt {n}}}} \ leq t_ {\alpha/2} ^ {n-1} \ Longleftrightarrow {\overline {X}} - t _ {\alpha/2} ^ {n-1} {\tfrac {S} {\ sqrt {n}}} \ leq \ mu \ leq {\ overline {X}} + t _ {\ alpha / 2} ^ {n-1} {\ tfrac {S} {\ sqrt {n}}}.}

Ad esempio, ecco le taglie misurate in cm su un campione di 8 persone

$io$	1	2	3	4	5	6	7	8
$x_ {i}$	155	160	161	167	171	177	180	181

calcoliamo la media statistica e la varianza senza distorsioni : $\ sopra {x}$ ${\ stile di visualizzazione ^ {2}}$

{\ displaystyle {\ overline {x}} = {\ frac {1} {8}} \ sum _ {i = 1} ^ {8} x_ {i} = 169}

{\ displaystyle s ^ {2} = {\ frac {1} {7}} \ sum _ {i = 1} ^ {8} (x_ {i} - {\ overline {x}}) ^ {2} = 96 {,} {\ sottolinea {857142}}}

Prendiamoci un rischio , quindi un livello di fiducia . All'arrotondamento più vicino, la tabella dei quantili seguente fornisce , e l'intervallo di confidenza è ${\ displaystyle \ alfa = 5 \%}$ ${\ displaystyle 1- \ alfa = 95 \%}$ ${\ displaystyle t_ {5 \%} ^ {7} = 1 {,} 895}$

{\ displaystyle \ left [{\ overline {x}} - t_ {5 \%} ^ {7} {\ frac {s} {\ sqrt {8}}}; {\ overline {x}} + t_ {5 \%} ^ {7} {\ frac {s} {\ sqrt {8}}} \ destra] = \ sinistra [162 {,} 4; 175 {,} 6 \ destra].}

La probabilità che la dimensione media della popolazione rientri in questo intervallo è del 90%. Tuttavia, l'altezza media dei francesi è di 177 cm, ma 177 non appartiene a questo intervallo di confidenza, possiamo quindi dire che questo campione non corrisponde alla popolazione francese, con un errore del 10%. Questo è un esempio dell'applicazione del test di Student .

Il grafico seguente illustra la nozione di livello di confidenza come integrale della funzione per , rappresentata dall'area della zona in blu. ${\ displaystyle f_ {T}}$ $k = 7$

In sintesi , per un campione di una distribuzione normale di aspettativa $μ$ , l'intervallo di confidenza di $μ$ al livello è: ${\ displaystyle x_ {1}, x_ {2}, ... x_ {n}}$ $1- \ alfa$

{\ displaystyle \ left [\, {\ overline {x}} - t _ {\ alpha / 2} ^ {n-1} {\ frac {s} {\ sqrt {n}}}, {\ overline {x } } + t _ {\ alpha / 2} ^ {n-1} {\ frac {s} {\ sqrt {n}}} \, \ destra]}

con

\ overline {x} = {\ frac {1} {n}} \ sum _ {{i = 1}} ^ {n} x_ {i}

{\ displaystyle s ^ {2} = {\ frac {1} {n-1}} \ sum _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2 }}

e il quantile d'ordine della legge di Student con $k$ gradi di libertà. ${\ displaystyle t _ {\ gamma} ^ {k}}$ ${\ displaystyle 1- \ gamma}$

Leggi correlate

$X \ sim {\ mathrm {t}} (k = 1) ~$ segue una distribuzione di Cauchy : . $X \ sim \ nomeoperatore {Cauchy} (0,1)$
${\ mathrm {t}} (k) \, {\ xrightarrow {{\ mathcal {L}}}} \, {\ mathcal {N}} (0,1)$ : La legge di Student converge in diritto verso la legge normale .
Se segue una legge di Student allora $X$ $2$ segue una legge di Fisher : $X \ sim {\ mathrm {t}} (k) \!$ $X ^ {2} \ sim \ nomeoperatore {F} (\ nu _ {1} = 1, \ nu _ {2} = k)$
$X \ sim {\ mathrm {t}} (k) ~$ ha la legge di Student se segue una legge inversa-χ² e segue una legge normale . $\ sigma ^ {2} \ sim {\ mbox {Inv -}} \ chi ^ {2} (k, 1) \!$ $X \ sim {\ mathcal {N}} (0, \ sigma ^ {2}) \!$

Tabella dei valori dei quantili

La tabella seguente fornisce i valori di alcuni quantili della legge di Student per diversi gradi di libertà k . Per ogni valore di , il quantile dato è tale che la probabilità che una variabile che segue una legge di Student con k gradi di libertà sia minore di . Quindi, per e k = 7, se $T$ segue una legge di Student con 7 gradi di libertà, si legge nella tabella che . Per un intervallo di scommessa bilaterale del 95%, sarà necessario il quantile del 97,5%: . ${\ displaystyle 1- \ alfa}$ ${\ displaystyle 1- \ alfa}$ ${\ displaystyle 1- \ alfa = 0 {,} 95}$ ${\ displaystyle \ mathbb {P} (T \ leq 1 {,} 895) = 0 {,} 95}$ ${\ displaystyle \ mathbb {P} (T \ in [-2 {,} 365; 2 {,} 365]) = 0 {,} 95}$

Nota anche che se indichiamo il quantile d' ordine della legge di Student con k gradi di libertà allora abbiamo . Con l'esempio precedente, abbiamo e ${\ displaystyle t _ {\ alpha} ^ {k}}$ $1- \ alfa$ ${\ displaystyle t _ {\ alpha} ^ {k} = - t_ {1- \ alpha} ^ {k}}$ ${\ displaystyle \ mathbb {P} (T \ leq 1 {,} 895) = 0 {,} 95}$ ${\ displaystyle \ mathbb {P} (T \ leq -1 {,} 895) = 0 {,} 05}$

Un foglio di calcolo standard consente di calcolare questi quantili in modo più preciso, ad esempio LOI.STUDENT.INVERSE(0,95;7)fornisce . Lo stesso valore è ottenuto con il comando del R software . In generale dà . ${\ displaystyle 1 {,} 89457860509001}$ qt(0.95,7)qt( $1-\alpha$ , $k$ ) ${\ displaystyle t _ {\ alpha} ^ {k}}$

$1 - α$	75%	80%	85%	90%	95%	97,5%	99%	99,5%	99,75%	99,9%	99,95%
K
1	1.000	1.376	1.963	3.078	6.314	12.71	31.82	63.66	127.3	318.3	636.6
2	0.816	1.061	1.386	1,886	2.920	4.303	6.965	9.925	14.09	22.33	31.60
3	0,765	0,978	1.250	1.638	2.353	3.182	4.541	5.841	7.453	10.21	12.92
4	0.741	0,941	1.190	1.533	2.132	2.776	3.747	4.604	5.598	7.173	8.610
5	0,727	0.920	1.156	1.476	2015	2,571	3.365	4.032	4.773	5.893	6.869
6	0,718	0,906	1.134	1.440	1.943	2,447	3.143	3.707	4.317	5.208	5.959
7	0,711	0,896	1.119	1,415	1.895	2.365	2.998	3.499	4.029	4.785	5.408
8	0,706	0,889	1.108	1.397	1.860	2.306	2.896	3.355	3.833	4.501	5.041
9	0,703	0,883	1.100	1.383	1.833	2.262	2.821	3,250	3.690	4.297	4.781
10	0,700	0,879	1.093	1,372	1.812	2.228	2.764	3.169	3.581	4.144	4.587
11	0,697	0,876	1.088	1.363	1.796	2.201	2.718	3.106	3.497	4.025	4.437
12	0,695	0,873	1.083	1.356	1.782	2.179	2.681	3.055	3.428	3.930	4.318
13	0,694	0,870	1.079	1.350	1.771	2.160	2.650	3.012	3.372	3.852	4.221
14	0,692	0,868	1.076	1.345	1.761	2.145	2.624	2.977	3.326	3.787	4.140
15	0,691	0,866	1.074	1.341	1.753	2.131	2.602	2.947	3.286	3.733	4.073
16	0,690	0,865	1.071	1,337	1.746	2.120	2,583	2.921	3.252	3.686	4.015
17	0,689	0,863	1.069	1.333	1.740	2.110	2,567	2.898	3.222	3.646	3.965
18	0,688	0,862	1.067	1.330	1.734	2.101	2,552	2.878	3.197	3.610	3.922
19	0,688	0,861	1.066	1.328	1.729	2.093	2,539	2.861	3.174	3.579	3.883
20	0,687	0,860	1.064	1.325	1.725	2.086	2,528	2.845	3.153	3.552	3,850
21	0,686	0,859	1.063	1.323	1.721	2.080	2.518	2.831	3.135	3.527	3.819
22	0,686	0,858	1.061	1.321	1.717	2.074	2.508	2.819	3.119	3.505	3.792
23	0,685	0,858	1.060	1.319	1.714	2.069	2.500	2.807	3.104	3,485	3.767
24	0,685	0,857	1.059	1.318	1.711	2.064	2.492	2.797	3.091	3.467	3.745
25	0,684	0.856	1.058	1.316	1.708	2.060	2.485	2.787	3.078	3,450	3.725
26	0,684	0.856	1.058	1.315	1.706	2.056	2,479	2.779	3.067	3.435	3.707
27	0,684	0,855	1.057	1.314	1.703	2.052	2.473	2,771	3.057	3.421	3.690
28	0,683	0,855	1.056	1.313	1.701	2.048	2,467	2.763	3.047	3.408	3.674
29	0,683	0,854	1.055	1.311	1.699	2.045	2,462	2.756	3.038	3.396	3.659
30	0,683	0,854	1.055	1.310	1.697	2.042	2.457	2.750	3.030	3.385	3.646
40	0,681	0,851	1.050	1.303	1,684	2.021	2,423	2.704	2,971	3.307	3.551
50	0.679	0,849	1.047	1.299	1.676	2.009	2.403	2.678	2.937	3.261	3.496
60	0.679	0,848	1.045	1.296	1,671	2.000	2.390	2.660	2.915	3.232	3.460
80	0,678	0,846	1.043	1.292	1.664	1.990	2.374	2.639	2.887	3.195	3.416
100	0,677	0,845	1.042	1.290	1.660	1.984	2.364	2.626	2.871	3.174	3.390
120	0,677	0,845	1.041	1.289	1.658	1.980	2.358	2.617	2.860	3.160	3.373
$\infty$	0,674	0.842	1.036	1.282	1.645	1.960	2.326	2,576	2.807	3.090	3.29129

Nota: l'ultima riga della tabella sopra corrisponde ai grandi valori di k . Si tratta di un caso limite per il quale la legge dello Studente è equivalente alla legge normale centrata e ridotta.

Vedi anche

Note e riferimenti

(it) Studente, " Il probabile errore della media era " , Biometrika , vol. 6, n ° 1,1908, pag. 1–25 ( DOI 10.2307 / 2331554 , JSTOR 2331554 )
(in) Joan Fisher Box, " Gosset, Fisher, and the t Distribution " , The American Statistician , vol. 35, n . 2maggio 1981, pag. 61-66 ( DOI 10.1080 / 00031305.1981.10479309 , JSTOR 2683142 )
(in) Ronald Fisher , " Applicazioni di" Student's "Distribution " , Metron , vol. 5,1925, pag. 90-104 ( letto online , consultato il 5 maggio 2018 )

Bibliografia

Gilbert Saporta , Probabilità, analisi dei dati e statistica , Parigi, Éditions Technip,2006, 622 pag. [ dettaglio delle edizioni ] ( ISBN 978-2-7108-0814-5 , presentazione online )