Teorema di Brooks

In matematica , specialmente nella teoria dei grafi , il teorema di Brooks dà una relazione tra il grado massimo di un grafo connesso non orientato e il numero cromatico .

Secondo questo teorema, in un grafo in cui ogni vertice ha al massimo Δ vicini , i vertici possono essere colorati con al massimo Δ colori, senza che due vertici adiacenti abbiano lo stesso colore, tranne in due casi, i grafi completi e i grafi dispari- cicli di lunghezza, che richiedono Δ + 1 colori.

stati

Teorema  -  In qualsiasi grafo connesso non orientato G di massimo grado Δ, il numero cromatico χ (G) soddisfa χ (G) ≤ Δ, a meno che G non sia un grafo completo o un ciclo di lunghezza dispari, nel qual caso χ (G) = Δ + 1.

Storia e background

Il teorema prende il nome da R. Leonard Brooks , che ne pubblicò una prova nel 1941. La colorazione con il numero di colori descritto dal teorema di Brooks è talvolta chiamata colorazione di Brooks o colorazione . László Lovász ha fornito una dimostrazione più semplice del teorema nel 1975.

Non è molto difficile mostrare che, per ogni grafo, χ (G) ≤ Δ + 1. Infatti, ogni vertice v ha al massimo Δ vertici vicini, che nel peggiore dei casi sono tutti colorati in modo diverso. Anche in questo caso, possiamo sempre prendere il (Δ + 1) esimo colore al colore v . Il merito di Brooks è stato quello di ridurre questo aumento di 1 unità nella maggior parte dei casi.

Dimostrazione

Ci sono diverse dimostrazioni del teorema di Brooks. Possiamo ad esempio ragionare per induzione sul numero di vertici del grafo. La seguente dimostrazione procede diversamente, si basa sull'algoritmo greedy per colorare i grafici e quindi ha il merito di fornire algoritmi per colorare il grafico (è una dimostrazione costruttiva ).

Questa dimostrazione è stata presentata da Ross Churchley nel 2010 sulla base del lavoro di John Adrian Bondy nel 2003. Il finale sostituisce il ragionamento di Bondy con altri lavori in modo da non dover fare appello prima ai risultati riguardanti gli alberi di alta gamma .

In quanto segue, esaminiamo successivamente quattro casi:

Caso di grafici non regolari

Il principio, nel caso di grafi non regolari , è quello di ordinare i vertici in un certo modo, per poi colorarli uno dopo l'altro utilizzando l' algoritmo greedy .

Numerazione, quindi colorazione di un grafico non regolare di massimo grado 4.

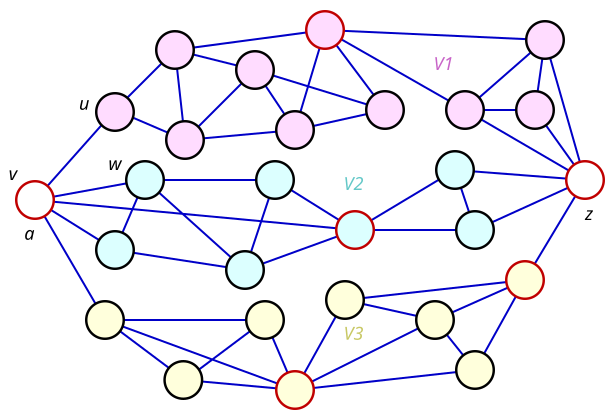
Sia G un grafo non regolare con n vertici e grado massimo . Poiché G non è regolare, esiste almeno un vertice x di grado s strettamente minore di . Mettiamo questo vertice alla fine della schedulazione, cioè v n = x (figura 1) . I vertici adiacenti a x sono posti appena prima in questo ordinamento, cioè in v n-s , v n-s-1 ,…, v n-1 (figura 2) .

Consideriamo poi i vertici adiacenti a v n-1 che non sono già stati ordinati (figura 3) , poi quelli adiacenti a v n-2 e che non sono ancora stati ordinati, e così via fino ad ordinarli tutti, che è possibile poiché G è connesso (figura 4) .

In questo ordinamento (v 1 , v 2 ,…, v n ) , tutti i vertici hanno almeno un vertice adiacente posteriore (di indice maggiore), eccetto il vertice x . Di conseguenza, hanno tutti, eccetto il vertice x , un numero di vertici adiacenti precedenti (di indice inferiore) strettamente minore di . Anche l'ultimo vertice x ha, per sua scelta iniziale, un numero di precedenti vertici adiacenti strettamente minore di .

Abbiamo poi il colore dei vertici v i uno dopo l'altro, per i che varia da 1 a n . Ad ogni passo, il vertice v i non è stato ancora colorato. I suoi precedenti vertici adiacenti, che sono già stati colorati, hanno un numero massimo di - 1, e quindi usano a fortiori un massimo di Δ - 1 colori. Possiamo quindi prendere per il nuovo vertice, nel peggiore dei casi, il colore rimanente tra (figure da 5 a 8) .

Caso di grafi regolari non biconnessi

In un grafo non biconnesso esiste almeno un punto di articolazione , cioè un vertice che, se rimosso, rende il grafo non connesso.

Colorazione di un grafico 3-regolare non biconnesso.

Consideriamo un tale grafo regolare G di grado non biconnesso e sia x un punto di articolazione di G (in rosso in figura 1).

Scomponiamo G moltiplicando il punto di articolazione come in Fig. 2. Otteniamo almeno due grafi non regolari collegati di massimo grado : infatti, i vertici ottenuti moltiplicando x sono ciascuno di grado strettamente minore di .

Si ritorna così al caso precedente e si può colorare ogni componente connesso non regolare utilizzando il metodo esposto in precedenza. Possiamo fare in modo che i vertici ottenuti moltiplicando x abbiano lo stesso colore: per questo, se necessario, scambiamo i colori all'interno dei componenti collegati.

Non resta che rimontare le parti del grafico per ottenere un grafico colorato con colori.

Caso di grafi regolari biconnessi di grado inferiore a 3

L'unico grafo regolare connesso di grado 0 è il grafo 0-regolare composto da un singolo vertice. Può essere colorato con 1 colore (figura 1) . Poiché rientra nella categoria dei grafi completi, soddisfa l'affermazione del teorema di Brooks.

L'unico grafo regolare di 1 grado connesso è il grafo regolare di 1 grado costituito da soli due vertici, con un bordo tra questi due vertici (figura 2) . Può essere colorato con 2 colori e anche qui siamo nel caso di un grafo completo: soddisfa l'affermazione del teorema di Brooks.

Gli unici grafici regolari collegati di grado 2 sono i cicli. I cicli con un numero pari di vertici possono essere colorati con 2 colori (figura 4) e sono necessari 3 colori per i cicli con un numero dispari di vertici (figure 3 e 5) . In entrambi i casi vale l'enunciato del teorema di Brooks.

Colorazione di grafici regolari collegati di grado 0, 1 o 2.

Caso di grafi regolari biconnessi di grado maggiore o uguale a 3

Se il grafo G è completo e di grado , ha Δ + 1 vertici che possiamo colorare con un colore diverso. Anche in questo caso vale l'enunciato del teorema di Brooks.

Se il grafico non è completo, ordineremo di nuovo un certo numero di vertici, quindi li coloreremo usando l'algoritmo greedy. Tuttavia, non è così semplice come nel caso del grafo non regolare, perché nulla garantisce a priori di avere un colore libero quando si arriva all'ultimo vertice. Faremo quindi in modo che l'ultimo vertice colorato v abbia due vicini u e w già colorati dello stesso colore, il che garantisce che avremo almeno un altro colore libero quando si tratta di colorare v .

Sia G un grafo biconnesso e incompleto di grado Δ ≥ 3. Ci sono tre vertici u , v e w tali che

Dimostrazione Lemma 1 In un grafo connesso e incompleto G, possiamo trovare vertici u e w vicini dello stesso vertice v , ma non vicini tra loro.

Poiché G non è completo, ci sono due vertici a e b che non sono direttamente collegati da un arco. Poiché il grafo è connesso, esiste un percorso ( a , v 1 , v 2 ,…, v p , b ) che collega a a b . Sia io il valore più grande tale che v i sia correlato a a . Considera u = a , v = v io e w = v io + 1 . Questi tre vertici verificano che u e w sono collegati a v senza essere collegati tra loro.

In un grafo connesso e incompleto, possiamo trovare u, v e w tali che u e w sono vicini di v, ma non sono vicini l'uno all'altro.

Poiché il grafo è biconnesso, possiamo rimuovere u o w da esso senza cessare di essere connesso: G - { u } e G - { w } sono connessi. Possiamo anche riuscire a prendere u , v e w tali che G - { u , w } sia ancora connesso.

Dimostrazione Lemma 2 In un grafo biconnesso G, di grado minimo 3 o superiore e non completo, possiamo trovare vertici u e w vicini allo stesso vertice v , ma non tra loro, in modo che G - { u , w } sia ancora connesso .

Poiché il grafo non è completo, esiste almeno un vertice a che non è adiacente a tutti gli altri.

Se G - { a } è biconnesso, prendiamo, come nella dimostrazione del Lemma 1, u = a e w uguale a qualsiasi vertice a distanza 2 da a . Poiché G - { a } è biconnesso, possiamo rimuovere w da esso senza perdere connettività e G - { u , w } è connesso.

Consideriamo ora il caso in cui G - { a } è connesso, ma non biconnesso. Ha quindi dei punti di articolazione (in rosso nella figura) . Sia z uno di questi punti di articolazione. G - { a , z } non è connesso, è addirittura suddiviso in almeno due componenti connesse disgiunte. Ognuna di queste componenti connesse V 1 , V 2 ,… V n può a sua volta essere tagliata in componenti biconnesse collegate dai punti di articolazione. Questi componenti biconnessi formano un albero con radice z .

Un grafo biconnesso che diventa non connesso quando rimuoviamo due dei suoi vertici a e z.

In G, a ha un vicino in ciascuna delle foglie alla fine di questo albero. Infatti, se togliamo il punto di articolazione z i a cui è collegata la foglia, se non fosse stato collegato ad una all'altra estremità, G - { z i } sarebbe estranea, che è impossibile, poiché G è biconnected.

Prendiamo u in una delle foglie alla fine di V 1 e w in una delle foglie alla fine di V 2 e sia v = a . I vertici u e w sono molto vicini a v . Non sono adiacenti, poiché sono presi da diversi componenti collegati.

I vertici u e w essendo presi in componenti biconnesse di G - { a } pur essendo diversi dai punti di articolazione di G - { a }, G - { a , u , w } rimane connesso. Poiché, inoltre, il grado di a è maggiore o uguale a 3, esiste un terzo vertice che consente di connettere a a G - { a , u , w }. Il grafo G - { u , w } è quindi connesso.

Poiché G - { u , w } è connesso, possiamo ordinarlo come nei casi precedenti assegnando a v il numero più forte. Quindi coloriamo G come segue:

Colorazione di un grafico regolare biconnesso di grado almeno 3 e non completo.

Quando arriviamo a colorare l'ultimo vertice v , abbiamo la garanzia che rimanga un colore libero, poiché i suoi due vicini u e w hanno lo stesso colore (figura 2) .

Risultati vicini

Una generalizzazione del teorema di Brooks si applica alla colorazione delle liste  : dato un grafo non orientato e connesso di massimo grado che non è né un grafo completo né un ciclo di lunghezza dispari, e una lista di Δ colori per ogni vertice, è possibile scegliere un colore per ogni vertice preso nella sua lista in modo che due vertici adiacenti non abbiano mai lo stesso colore. In altre parole, il numero cromatico di lista di un grafo connesso non orientato non è mai maggiore di , tranne nel caso di un grafo completo o di un ciclo di lunghezza dispari. Questo è stato dimostrato da Vadim Vizing nel 1976.

Con alcuni grafici, abbiamo anche bisogno di meno Δ colori. Bruce Reed mostra che Δ - 1 colori sono sufficienti se e solo se il grafico non ha Δ- clic quando è sufficientemente grande. Per grafi senza triangolo (senza un insieme di tre vertici adiacenti in coppia), o più in generale per grafi in cui l' intorno di ciascun vertice è sufficientemente vuoto , sono sufficienti i colori O (Δ / log Δ).

Il grado di un grafico compare anche nei limiti superiori del numero di colori richiesti per altri tipi di colorazione:

Algoritmi

Una colorazione con Δ colori, o anche una colorazione per lista con Δ colori, di un grafo di massimo grado Δ può essere ottenuta in un tempo lineare (proporzionale al numero di vertici e spigoli). Sono noti anche algoritmi efficienti che consentono di trovare le macchie di Brooks utilizzando l'elaborazione parallela o distribuita.

Note e riferimenti

  1. (in) RL Brooks , "  sta colorando i nodi di una rete  " , Proc. Società filosofica di Cambridge, matematica. Fis. Sci. , vol.  37,1941, pag.  194-197 ( leggi online ).
  2. (in) L. Lovász , "  Tre brevi dimostrazioni nella teoria dei grafi  " , J. Combin. Th., Serie B , vol.  19,1975, pag.  269–271 ( DOI  10.1016 / 0095-8956 (75) 90089-1 )
  3. (in) Ross Churchley, "  Haiku di teoria dei grafi - Tre cortometraggi e belle prove  ", novembre 2010.
  4. (in) JA Bondy , "  Brevi dimostrazioni di teoremi classici  " , Journal of Graph Theory , vol.  44, n .  3,novembre 2003, pag.  da 159 a 165
  5. (in) Bradley Baetz e David R. Wood, "  Brooks Vertex-Coloring Theorem in Linear Time , Technical Report CS-AAG-2001-05, The University of Sydney, October 2001.
  6. (in) Dieter Jungnickel, "  Grafici, reti e algoritmi  ", volume 5, seconda edizione, Springer Verlag, maggio 2003 ( ISBN  3-540-63760-5 ) .
  7. (ru) VG Vizing , “  Colori vertici con colori dati  ” , Diskret. Analizza. , vol.  29,1976, pag.  3–10
  8. (in) Bruce Reed , "  Un rafforzamento del teorema di Brooks  " , J. Combin. Th., Serie B , vol.  76, n .  21999, pag.  136–149 ( DOI  10.1006 / jctb.1998.1891 )
  9. (in) Noga Alon Michael Krivelevich e Benny Sudakov , "  Grafici da colorare con quartieri sparsi  " , J. Combin. Th., Serie B , vol.  77, n °  1,1999, pag.  73–82 ( DOI  10.1006 / jctb.1999.1910 )
  10. (in) San Skulrattanakulchai , "  -Lista colorazione dei vertici in tempo lineare  " , Inf. Processi. Lett. , vol.  98, n .  3,2006, pag.  101–106 ( DOI  10.1016 / j.ipl.2005.12.007 )
  11. (in) HJ Karloff , "  Un algoritmo per il teorema di NC Brooks  " , TCS , vol.  68, n °  1,1989, pag.  89-103 ( DOI  10.1016 / 0304-3975 (89) 90121-7 )
  12. (in) Péter Hajnal e Endre Szemerédi , "  Brooks che colora in parallelo  " , SIAM J. Discrete Math. , vol.  3, n °  1,1990, pag.  74–80 ( DOI  10.1137 / 0403008 )
  13. (in) Alessandro Panconesi e Aravind Srinivasan , "  Il tipo locale di -colorazione e le sue applicazioni algoritmiche  " , combinatorica , vol.  15, n o  21995, pag.  255–280 ( DOI  10.1007 / BF01200759 )
  14. (in) David A. Grable e Alessandro Panconesi , "Algoritmi veloci per colorazioni Brooks-Vizing distribuite" in SODA '98: Atti del 9° Simposio annuale ACM-SIAM sugli algoritmi discreti , Philadelphia, PA, USA, SIAM , al.  "Journal of Algorithms" ( n o  37),1998( DOI  10.1006 / jagm.2000.1097 , leggi online )

Link esterno

(it) Eric W. Weisstein , "  Brooks' Theorem  " , su MathWorld