Legge geometrica

Legge geometrica
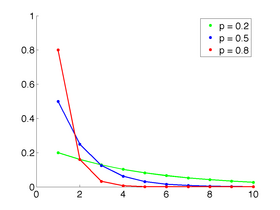Funzione di massa
Funzione di distribuzione
impostazioni	p∈[0,1]{\ displaystyle p \ in [0,1]} q=1-p{\ displaystyle q = 1-p}
Supporto	K∈{1,2,3,...}{\ Displaystyle k \ in \ {1,2,3, \ dots \} \!}
Funzione di massa	qK-1p{\ displaystyle q ^ {k-1} \, p \!}
Funzione di distribuzione	1-qK{\ displaystyle 1-q ^ {k} \!}
Speranza	1p{\ displaystyle {\ frac {1} {p}} \!}
Mediano	⌈-log⁡(2)log⁡(q)⌉{\ displaystyle \ left \ lceil {\ frac {- \ log (2)} {\ log (q)}} \ right \ rceil \!}(non univoco se è intero) -log⁡(2)/log⁡(q){\ displaystyle - \ log (2) / \ log (q)}
Moda	1
Varianza	qp2{\ displaystyle {\ frac {q} {p ^ {2}}} \!}
Asimmetria	2-pq{\ displaystyle {\ frac {2-p} {\ sqrt {q}}} \!}
Curtosi normalizzata	6+p2q{\ displaystyle 6 + {\ frac {p ^ {2}} {q}} \!}
Entropia	-qlog2⁡q-plog2⁡pp{\ displaystyle {\ frac {-q \ log _ {2} qp \ log _ {2} p} {p}} \!}
Funzione generatrice di momenti	pet1-qet{\ displaystyle {\ frac {pe ^ {t}} {1-q \, e ^ {t}}} \!}
Funzione caratteristica	peiot1-qeiot{\ displaystyle {\ frac {pe ^ {it}} {1-q \, e ^ {it}}} \!}
Funzione generatrice di probabilità	pt1-qt{\ displaystyle {\ frac {pt} {1-qt}}}

In teoria e statistica della probabilità , la legge geometrica è una legge di probabilità discreta con due possibili definizioni:

• la legge del numero X dei test di Bernoulli indipendenti con probabilità di successo p ∈] 0.1 [ (oppure q = 1 - p di fallimento) necessaria per ottenere il primo successo. X è la variabile casuale che dà il rango del primo successo. Il supporto della legge è quindi {1, 2, 3, ...}.
• La legge del numero Y = X - 1 fallimenti prima del primo successo. Il supporto della legge è quindi {0, 1, 2, 3, ...}.

I valori di X sono gli interi naturali diversi da zero 1, 2, 3, ... Notando , la probabilità che X = k sia quindi, per k = 1, 2, 3, ...: q=1-p{\ displaystyle q = 1-p}

P(X=K)=qK-1p.{\ Displaystyle \ mathbb {P} (X = k) = q ^ {k-1} p.}

Diciamo che X segue una legge geometrica con parametro p .

Calcolo di p ( k )

La probabilità p ( k ) corrisponde alla probabilità di ottenere in una successione di k test di Bernoulli , k - 1 fallimenti seguiti da un successo. Poiché i test sono indipendenti, questa probabilità è q k - 1 p .

Altra definizione

Per la legge geometrica, talvolta incontriamo questa definizione: la probabilità p ' ( k ) è la probabilità, durante una successione di test di Bernoulli indipendenti, di ottenere k fallimenti seguiti da un successo. Modella la durata della vita di un'entità che avrebbe la probabilità p di morire in qualsiasi momento . Otteniamo quindi, per k = 0, 1, 2, ...:

p′(K)=qKp.{\ displaystyle p '(k) = q ^ {k} p.}

Si noti che questo è solo uno spostamento della legge geometrica precedente, nel seguente senso: se X segue la legge p allora X - 1 segue la legge p ' . La sua speranza allora non è più1/p ma di 1/p- 1 , vale a direq/p. La varianza è la stessa per entrambe le definizioni. Di seguito, prenderemo la prima definizione.

Data di morte, durata della vita

Se chiamiamo p la probabilità di decadimento di una particella radioattiva, la legge geometrica è il primo modello discreto della morte di una particella radioattiva. La durata della particella radioattiva V segue la seguente legge di probabilità:

p(K)=P(V=K)=qK-1 pour K∈NON∗{\ displaystyle p (k) = \ mathbb {P} (\ mathrm {V} = k) = q ^ {k-1} \ \ mathrm {per} \ k \ in \ mathbb {N} ^ {*}}

P(V>K)=qK=eKln⁡(q){\ Displaystyle \ mathbb {P} (\ mathrm {V}> k) = q ^ {k} = \ mathrm {e} ^ {k \ ln (q)}}

Per p piccolo, ln (1 - p ) è vicino a - p così

P(V>K)≈e-pK{\ Displaystyle \ mathbb {P} (\ mathrm {V}> k) \ approx \ mathrm {e} ^ {- pk}}

dove troviamo la distribuzione della legge esponenziale .

Aspettativa, varianza, deviazione standard

L' aspettativa di una variabile casuale X che segue una distribuzione geometrica del parametro p è 1 ⁄ p , e la sua varianza èq/p 2dove q = 1 - p è la probabilità di fallimento:

E[X]=1p,V[X]=1-pp2=qp2.{\ displaystyle \ mathbb {E} [X] = {\ frac {1} {p}}, \ qquad \ mathbb {V} [X] = {\ frac {1-p} {p ^ {2}}} = {\ frac {q} {p ^ {2}}}.}

La deviazione standard è quindi√ q/p.

Calcoli preliminari: per tutte le x di [0, 1 [ ,

f(X)=∑K=0+∞XK=11-Xf′(X)=∑K=1+∞KXK-1=1(1-X)2f′′(X)=∑K=2+∞K(K-1)XK-2=2(1-X)3.{\ displaystyle {\ begin {align} f (x) & = \ sum _ {k = 0} ^ {+ \ infty} x ^ {k} = {\ frac {1} {1-x}} \\ f ^ {\ prime} (x) & = \ sum _ {k = 1} ^ {+ \ infty} kx ^ {k-1} = {\ frac {1} {(1-x) ^ {2}}} \\ f ^ {\ prime \ prime} (x) & = \ sum _ {k = 2} ^ {+ \ infty} k (k-1) x ^ {k-2} = {\ frac {2} { (1-x) ^ {3}}}. \ End {allineato}}}

In particolare :

∑K=1+∞K2XK-1=X∑K=2+∞K(K-1)XK-2+∑K=1+∞KXK-1=2X(1-X)3+1(1-X)2=2(1-X)3-1(1-X)2.{\ displaystyle {\ begin {align} \ sum _ {k = 1} ^ {+ \ infty} k ^ {2} x ^ {k-1} & = x \ sum _ {k = 2} ^ {+ \ infty} k (k-1) x ^ {k-2} + \ sum _ {k = 1} ^ {+ \ infty} kx ^ {k-1} \\ & = {\ frac {2x} {(1 -x) ^ {3}}} + {\ frac {1} {(1-x) ^ {2}}} \\ & = {\ frac {2} {(1-x) ^ {3}}} - {\ frac {1} {(1-x) ^ {2}}}. \ end {align}}}

Possiamo quindi utilizzare queste identità per il calcolo dell'aspettativa:

E(X)=∑K=1+∞KqK-1p=p(1-q)2=1p,{\ displaystyle {\ begin {align} \ mathbb {E} (X) & = \ sum _ {k = 1} ^ {+ \ infty} kq ^ {k-1} p \\ & = {\ frac {p } {(1-q) ^ {2}}} \\ & = {\ frac {1} {p}}, \ end {align}}}

perché q = 1 - p , e per quello della varianza:

Var(X)=(∑K=1+∞K2qK-1p)-E[X]2=2p(1-q)3-p(1-q)2-1p2=2p2-1p-1p2=qp2,{\ displaystyle {\ begin {align} \ mathrm {Var} (X) & = \ left (\ sum _ {k = 1} ^ {+ \ infty} k ^ {2} q ^ {k-1} p \ destra) - \ mathbb {E} [\ mathrm {X}] ^ {2} \\ & = {\ frac {2p} {(1-q) ^ {3}}} - {\ frac {p} {( 1-q) ^ {2}}} - {\ frac {1} {p ^ {2}}} \\ & = {\ frac {2} {p ^ {2}}} - {\ frac {1} {p}} - {\ frac {1} {p ^ {2}}} \\ & = {\ frac {q} {p ^ {2}}}, \ end {align}}}

la prima uguaglianza sopra derivante dal teorema di König-Huygens .

Ad esempio, per , e la deviazione media . p=1/2{\ displaystyle p = 1/2}E[X]=2,V[X]=2,σ[X]=2{\ displaystyle \ mathbb {E} [X] = 2, \ mathbb {V} [X] = 2, \ sigma [X] = {\ sqrt {2}}} EM(X)=E(|X-2|)=∑K=1+∞|K-2|/2K=1{\ displaystyle {\ textbf {EM}} (X) = \ mathbb {E} (| X-2 |) = \ sum _ {k = 1} ^ {+ \ infty} {| k-2 | / 2 ^ {k}} = 1}

Collegamenti ad altre leggi

Legame con la legge geometrica troncata

Nei programmi 2011 di Première Scientifique in Francia, che noi chiamiamo la legge geometrica troncato di parametri n e p , la legge della variabile casuale ottenuto limitando il numero di prove di Bernoulli di parametro p a n e notando il rango del primo successo. . Per convenzione, se non si verifica alcun successo durante gli n test, poniamo X = 0 (a volte troviamo per X il numero di fallimenti ottenuti durante gli n test). La probabilità che X = k sia quindi, per k = 1, 2, 3, ..., n  :

P(X=K)=qK-1p{\ displaystyle \ mathbb {P} (X = k) = q ^ {k-1} p}

e per k = 0

P(X=0)=qnon.{\ displaystyle \ mathbb {P} (X = 0) = q ^ {n}.}

Questa legge della probabilità ha per aspettativa: E(X)=1p(1-(nonp+1)qnon){\ displaystyle \ mathbb {E} (X) = {\ frac {1} {p}} \ sinistra (1- \ sinistra (np + 1 \ destra) q ^ {n} \ destra)} dove q = 1 - p .

Il termine "troncato" qui non ha lo stesso significato di quello che si trova nella definizione di una legge troncata .

Collegamento con la legge esponenziale

La legge geometrica è una versione discretizzata della legge esponenziale. Di conseguenza, la legge esponenziale è un limite delle leggi geometriche rinormalizzate.

Proprietà  -  Se X segue la legge esponenziale dell'aspettativa 1 e se allora Y segue la legge geometrica del parametro Y=⌈θX⌉, θ>0,{\ Displaystyle Y = \ lceil \ theta X \ rceil, \ \ theta> 0,}

p = 1-e- 1θ.{\ displaystyle p \ = \ 1- \ mathrm {e} ^ {- \ {\ tfrac {1} {\ theta}}}.}

P(Y=K)=P(⌈θX⌉=K)=P(θX∈]K-1,K])=P(X∈]K-1θ,Kθ])=FX(Kθ)-FX(K-1θ)=exp⁡(- K-1θ)-exp⁡(- Kθ)=(e- 1θ)K-1 (1-e- 1θ).{\ displaystyle {\ begin {align} \ mathbb {P} (Y = k) & = \ mathbb {P} (\ lceil \ theta X \ rceil = k) \\ & = \ mathbb {P} (\ theta X \ in] k-1, k]) \\ & = \ mathbb {P} \ left (X \ in \ left] {\ tfrac {k-1} {\ theta}}, {\ tfrac {k} {\ theta}} \ right] \ right) \\ & = F_ {X} \ left ({\ tfrac {k} {\ theta}} \ right) -F_ {X} \ left ({\ tfrac {k-1} {\ theta}} \ right) \\ & = \ exp \ left (- \ {\ tfrac {k-1} {\ theta}} \ right) - \ exp \ left (- \ {\ tfrac {k} { \ theta}} \ right) \\ & = \ left (\ mathrm {e} ^ {- \ {\ tfrac {1} {\ theta}}} \ right) ^ {k-1} \ \ left (1- \ mathrm {e} ^ {- \ {\ tfrac {1} {\ theta}}} \ right). \ end {align}}}

Si noti che, per un numero reale x , denota la parte intera superiore di x , definita da ⌈X⌉{\ displaystyle \ lceil x \ rceil}

⌈X⌉ = min{K∈Z | K⩾X}.{\ displaystyle \ lceil x \ rceil \ = \ \ min \ sinistra \ {k \ in \ mathbb {Z} \ | \ k \ geqslant x \ right \}.}

Quindi, per ottenere una variabile casuale Y ' secondo una legge geometrica di parametro arbitrario p (con comunque il vincolo 0 < p <1 ), da una variabile casuale esponenziale X' di parametro λ , è sufficiente impostare

Y′=⌈θX′⌉,{\ displaystyle Y ^ {\ prime} = \ lceil \ theta X ^ {\ prime} \ rceil,}

dove abbiamo scelto

θ = -λln⁡(1-p).{\ displaystyle \ theta \ = \ - {\ tfrac {\ lambda} {\ ln \ left (1-p \ right)}}.}

In effetti, segue una legge esponenziale del parametro 1 (e aspettativa 1). X=λX′{\ displaystyle X = \ lambda \, X ^ {\ prime}}

Reciprocamente,

Proprietà  -  Se, per la variabile casuale Y n segue la legge geometrica del parametro p n , e se, contemporaneamente, non≥1,{\ displaystyle n \ geq 1,}

limnonpnon = 0elimnonpnon/anon = λ>0,{\ displaystyle \ lim _ {n} p_ {n} \ = \ 0 \ qquad {\ text {et}} \ qquad \ lim _ {n} p_ {n} / a_ {n} \ = \ \ lambda> 0 ,}

allora a n Y n converge di diritto verso la legge esponenziale del parametro λ .

Diamo a noi stessi una variabile casuale esponenziale X con parametro 1 e impostiamo

θnon=-1ln⁡(1-pnon),Ynon′=⌈θnonX⌉.{\ displaystyle {\ begin {align} \ theta _ {n} & = - {\ tfrac {1} {\ ln \ left (1-p_ {n} \ right)}}, \\\ mathrm {Y} _ {n} ^ {\ prime} & = \ lceil \ theta _ {n} \ mathrm {X} \ rceil. \ end {allineato}}}

Quindi Y n e hanno la stessa legge, in virtù della proprietà precedente. Inoltre, per tutti ωYnon′{\ displaystyle Y_ {n} ^ {\ prime}}

limnonanonYnon′(ω) = limnonanon⌈θnonX(ω)⌉= (limnonanonθnon) X(ω) = X(ω)/λ.{\ displaystyle \ lim _ {n} a_ {n} Y_ {n} ^ {\ prime} (\ omega) \ = \ \ lim _ {n} a_ {n} \ lceil \ theta _ {n} X (\ omega) \ rceil = \ \ left (\ lim _ {n} a_ {n} \ theta _ {n} \ right) \ X (\ omega) \ = \ X (\ omega) / \ lambda.}

Tuttavia, da un lato, una convergenza quasi sicura porta alla convergenza in legge, dall'altro la legge di X / λ è la legge esponenziale del parametro λ .

Legame con la legge binomiale negativa

Se X n è una variabile casuale distribuita secondo i parametri binomiali negativi n e p , allora X n ha la stessa distribuzione della somma di n variabili casuali indipendenti distribuite in una distribuzione geometrica con parametro p .

Vedi anche

• Variabili casuali elementari
• Radioattività
• Metodo di rigetto
• Processo di Bernoulli
• Legge esponenziale
• Legge binomiale negativa
• Problema del collezionista di vignette (un esempio che mostra una legge geometrica)

Note e riferimenti

1. Éduscol documento di risorse - Statistica e probabilità - giugno 2011 , pp. 13-24
2. Corso di probabilità 2011/2012 dell'UJF di Grenoble, p. 7